3.3. Расчет равновесной степени конверсии метана.
Из принципа Ле Шателье следует, что высокие
степени превращения метана ![]() 2 в суммарном
эндотермическом процессе, описываемом
уравнениями (1) и (2), могут быть достигнуты за счет
увеличения отношения пар : метан
2 в суммарном
эндотермическом процессе, описываемом
уравнениями (1) и (2), могут быть достигнуты за счет
увеличения отношения пар : метан ![]() в сырьевом потоке и повышения температуры за
счет подвода теплоты к реактору. Очевидно, что
особое значение для глубины протекания реакции
(1) имеет повышение температуры на концевом
участке реакционной трубы. Если предположить,
что на достаточно протяженном участке трубы,
примыкающем к выходу газов, поддерживается (за
счет целенаправленной организации теплоподвода
к реакционным трубам) постоянная температура Т2
, то следует ожидать, что в реагирующей смеси
установится равновесное не только по отношению к
быстрой реакции (2), но и относительно медленной
реакции (1), соотношение концентраций всех
реагентов. На языке математического
моделирования такое предположение означает
постановку дополнительного граничного условия
"на полубесконечности", т.е. на бесконечном
удалении от входа потока в систему.
Использование абстракции
"полубесконечного" реактора позволяет,
основываясь лишь на элементарных уравнениях
материального баланса, провести очень важные при
проектировании или оптимизации реактора расчеты
максимальной для каждого температурного уровня
степени конверсии метана.
в сырьевом потоке и повышения температуры за
счет подвода теплоты к реактору. Очевидно, что
особое значение для глубины протекания реакции
(1) имеет повышение температуры на концевом
участке реакционной трубы. Если предположить,
что на достаточно протяженном участке трубы,
примыкающем к выходу газов, поддерживается (за
счет целенаправленной организации теплоподвода
к реакционным трубам) постоянная температура Т2
, то следует ожидать, что в реагирующей смеси
установится равновесное не только по отношению к
быстрой реакции (2), но и относительно медленной
реакции (1), соотношение концентраций всех
реагентов. На языке математического
моделирования такое предположение означает
постановку дополнительного граничного условия
"на полубесконечности", т.е. на бесконечном
удалении от входа потока в систему.
Использование абстракции
"полубесконечного" реактора позволяет,
основываясь лишь на элементарных уравнениях
материального баланса, провести очень важные при
проектировании или оптимизации реактора расчеты
максимальной для каждого температурного уровня
степени конверсии метана.
Для этого достаточно разрешить относительно ![]() 2
уравнение, описывающее равновесие по первой
реакции (равновесие по второй реакции уже учтено
в выражении (16):
2
уравнение, описывающее равновесие по первой
реакции (равновесие по второй реакции уже учтено
в выражении (16):
| КР,1(Т2 ) = | 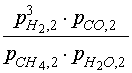 |
= | 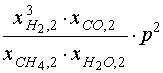 , (17) , (17) |
где р – общее давление в реакционных
трубах. Мольные доли определяются по уравнению
(14). Зависимость константы равновесия КР,1
от температуры описывается выражением,
приведенным в табл.1. Уравнение (17) неявным
образом определяет искомую зависимость ![]() 2
от Т2. Решение этого уравнения
относительно
2
от Т2. Решение этого уравнения
относительно ![]() 2 , ввиду его нелинейности и
зависимости правой части от Т2 (через
входящую в выражения для мольных долей величину
2 , ввиду его нелинейности и
зависимости правой части от Т2 (через
входящую в выражения для мольных долей величину ![]() 2 ),
может быть проведено тем или иным численным
способом – путем подбора величины
2 ),
может быть проведено тем или иным численным
способом – путем подбора величины ![]() 2
при фиксированной температуре Т2 .
2
при фиксированной температуре Т2 .
Упражнение.
Составьте программу расчета на компьютере
равновесной степени конверсии метана ![]() 2 при
произвольных значениях Т2 , р и
2 при
произвольных значениях Т2 , р и ![]() , воспользовавшись нижеследующим
описанием алгоритма расчета.
, воспользовавшись нижеследующим
описанием алгоритма расчета.
Уравнение (17) представим в виде
| F( |
КР,1(Т2) – f( |
| где f( |
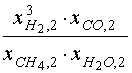 |
При фиксированных значениях Т2 , р и ![]() для нахождения решения
для нахождения решения ![]() 2 уравнения (17а)
воспользуемся методом дихотомии (методом
деления отрезка пополам). В интервале (0, 1)
выбираются два значения
2 уравнения (17а)
воспользуемся методом дихотомии (методом
деления отрезка пополам). В интервале (0, 1)
выбираются два значения ![]() 2 , при которых знаки F(
2 , при которых знаки F(![]() 2 ,Т2,
p) различаются (следовательно, корень уравнения
(17а) находится между выбранными значениями
2 ,Т2,
p) различаются (следовательно, корень уравнения
(17а) находится между выбранными значениями ![]() 2 ),
затем исследуется знак F(
2 ),
затем исследуется знак F(![]() 2 ,Т2, p) посередине
между этими значениями. Таким образом,
исследуемый интервал значений
2 ,Т2, p) посередине
между этими значениями. Таким образом,
исследуемый интервал значений ![]() 2 сужается вдвое: он
выбирается между средним и одним из начальных
значений
2 сужается вдвое: он
выбирается между средним и одним из начальных
значений ![]() 2
так, чтобы знаки F(
2
так, чтобы знаки F(![]() 2 ,Т2, p) при них были
различны. Процедура деления исследуемого
интервала пополам продолжается до тех пор, пока
не будет достигнута заданная точность
определения величины
2 ,Т2, p) при них были
различны. Процедура деления исследуемого
интервала пополам продолжается до тех пор, пока
не будет достигнута заданная точность
определения величины ![]() 2 .
2 .
На рис.3 представлены рассчитанные зависимости
равновесной степени превращения метана ![]() 2(Т2)
при разных давлениях р и отношениях
2(Т2)
при разных давлениях р и отношениях ![]() .
.
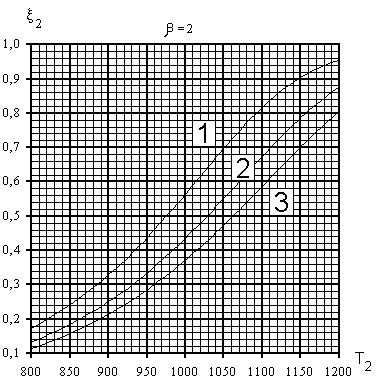
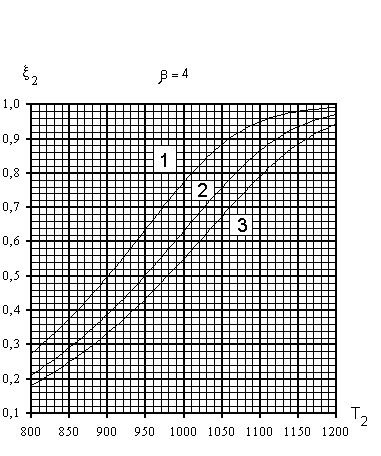
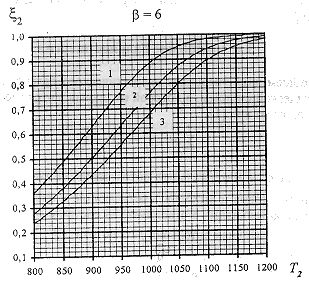
Рис 3. Зависимости равновесной степени
превращения метана ![]() 2 от температуры Т2
на выходе реакционных труб Т.П. при различных
значениях параметра и давления : 1- р =10 атм,
2-20 атм, 3 - р = 30 атм
2 от температуры Т2
на выходе реакционных труб Т.П. при различных
значениях параметра и давления : 1- р =10 атм,
2-20 атм, 3 - р = 30 атм
Как видно, равновесная степень конверсии
метана возрастает при увеличении Т2 и ![]() и при уменьшении общего давления р
. Однако имеются технические ограничения на
область изменения этих параметров. Увеличение
температуры ограничено термической
устойчивостью конструкции Т.П. и связано с
повышением расхода сжигаемого топлива.
Максимальная рабочая температура стенок
реакционных труб современных трубчатых печей не
должна превышать 900 - 930оС [2, 3, 4].
Увеличение параметра
и при уменьшении общего давления р
. Однако имеются технические ограничения на
область изменения этих параметров. Увеличение
температуры ограничено термической
устойчивостью конструкции Т.П. и связано с
повышением расхода сжигаемого топлива.
Максимальная рабочая температура стенок
реакционных труб современных трубчатых печей не
должна превышать 900 - 930оС [2, 3, 4].
Увеличение параметра ![]() влечет за
собой увеличение объемов аппаратов, повышение
расходов энергии на приготовление пара и на
преодоление механического трения при движении
смеси через аппараты. Снижение давления приводит
к уменьшению скоростей химических реакций и
увеличению требуемых объемов аппаратов. В
заключение отметим, что в действующих трубчатых
печах, несмотря на высокие объемные скорости
протекания газовой смеси через реакционные
трубы, достигается степень превращения метана,
близкая к равновесной [3, 4]
влечет за
собой увеличение объемов аппаратов, повышение
расходов энергии на приготовление пара и на
преодоление механического трения при движении
смеси через аппараты. Снижение давления приводит
к уменьшению скоростей химических реакций и
увеличению требуемых объемов аппаратов. В
заключение отметим, что в действующих трубчатых
печах, несмотря на высокие объемные скорости
протекания газовой смеси через реакционные
трубы, достигается степень превращения метана,
близкая к равновесной [3, 4]
3.4. Уравнение баланса энергии.
В общем виде уравнение энергетического баланса для химико-технологической системы, в которой не производится (не потребляется) работа, имеет вид [1]:
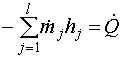 , (18)
, (18)
где ![]() , кг с-1 -
материальный поток через j-й вход или выход, l
- общее число входов и выходов; поступающие в
систему потоки считаются положительными, а
отводимые из системы - отрицательными;
, кг с-1 -
материальный поток через j-й вход или выход, l
- общее число входов и выходов; поступающие в
систему потоки считаются положительными, а
отводимые из системы - отрицательными; ![]() , Дж кг-1 - удельная
энтальпия j-го потока;
, Дж кг-1 - удельная
энтальпия j-го потока; ![]() , Дж с-1 - скорость подвода теплоты к
системе.
, Дж с-1 - скорость подвода теплоты к
системе.
Абсолютная величина каждого из слагаемых в сумме в левой части (18) для случая, когда потоки представляют собой смеси идеальных газов (тепловой эффект смешения которых равен нулю), может быть рассчитана как
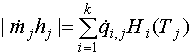 , (19)
, (19)
где ![]() , моль с-1-
абсолютное значение потока i-го вещества
через j-й вход или выход системы;
, моль с-1-
абсолютное значение потока i-го вещества
через j-й вход или выход системы; ![]() , Дж моль-1 - молярная энтальпия
i-го вещества при температуре
, Дж моль-1 - молярная энтальпия
i-го вещества при температуре ![]() , К ;
, К ; ![]() -
число химических компонентов в j-м потоке
системы.
-
число химических компонентов в j-м потоке
системы.
Применительно к реакционным трубам Т.П. уравнение баланса энергии примет форму
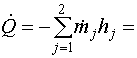 |
+ | + | + |
|
+ |
- | - |
где j = 1 относится ко входу, j = 2 - к выходу из реакционных труб.
Подставив найденные в предыдущем разделе выражения (9)-(12) для выходящих потоков, получим:
| + | + | ||||
| + | + | + | |||
| + | - | |
- | |
В приближенных расчетах в уравнение (21) в качестве молярной энтальпии i-го идеального газа Hi(T), в предположении постоянства теплоемкости газа Сp,i , можно подставлять величину
![]() H0f,i + Сp,i
(T - 298),
H0f,i + Сp,i
(T - 298),
где ![]() H0f,i -
стандартная энтальпия образования i-го
вещества при Т = 298 K (так как в уравнение
энергетического баланса входят разности
энтальпий для веществ, построенных из одних и тех
же химических элементов [1, п.3.2] ).
H0f,i -
стандартная энтальпия образования i-го
вещества при Т = 298 K (так как в уравнение
энергетического баланса входят разности
энтальпий для веществ, построенных из одних и тех
же химических элементов [1, п.3.2] ).
Уравнение (21) можно упростить и привести к более компактному и удобному для расчетов виду. Для этого сгруппируем входящие в уравнение энтальпии веществ таким образом, чтобы выделить тепловые эффекты линейно независимых реакций (1) и (2), выбранных для описания процесса конверсии:
![]() =
= ![]() {
{![]() 2
[3HH2(T2)+HCO(T2)
- HCH4(T2) - HH2O(T2)]+
2
[3HH2(T2)+HCO(T2)
- HCH4(T2) - HH2O(T2)]+
+![]() 2 [HH2(T2)+HCO2(T2)
- HCO(T2) - HH2O(T2)]
+
2 [HH2(T2)+HCO2(T2)
- HCO(T2) - HH2O(T2)]
+
+ [HCH4 (Т2) - HCH4 (Т1)]+
![]() [HH2O (Т2) - HH2O
(Т1)]} ;
[HH2O (Т2) - HH2O
(Т1)]} ;
или
![]() =
= ![]() {[HCH4(Т2 )-HCH4 (Т1)]
+
{[HCH4(Т2 )-HCH4 (Т1)]
+![]() [HH2O(Т2 )-HH2O(Т1
)]+
[HH2O(Т2 )-HH2O(Т1
)]+
+ ![]() 2
2 ![]() 1H(Т2)+
1H(Т2)+ ![]() 2
2 ![]() 2H(Т2)} , (22)
2H(Т2)} , (22)
где ![]() rH (r = 1, 2) -
изменение энтальпии соответственно при реакции
(1) и (2).
rH (r = 1, 2) -
изменение энтальпии соответственно при реакции
(1) и (2).
Уравнение (22) имеет ясный физический смысл,
показывая, что результирующее превращение
веществ в реакционных трубах можно мысленно
представить как последовательный нагрев
питающих потоков метана ![]() и воды
и воды ![]() =
= ![]()
![]() от
начальной температуры Т1 до конечной Т2
, превращение по реакции (1) при температуре Т2
части потока метана
от
начальной температуры Т1 до конечной Т2
, превращение по реакции (1) при температуре Т2
части потока метана ![]() 2
2![]() и, наконец, превращение по реакции (2) при
температуре Т2 части потока
образовавшегося СО, равной потоку конечного
продукта
и, наконец, превращение по реакции (2) при
температуре Т2 части потока
образовавшегося СО, равной потоку конечного
продукта ![]() =c 2
=c 2 ![]() .
.
Уравнение баланса энергии (22) можно записать в виде
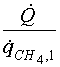 |
= [HCH4(Т2 )-HCH4 (Т1)]+ | + | + |
где ![]() имеет смысл количества
подведенной теплоты в расчете на 1 моль
поступающего в реактор метана. Полученное
уравнение, с учетом соотношения (16), позволяет
рассчитать требуемый поток теплоты для
достижения заданной степени конверсии метана
имеет смысл количества
подведенной теплоты в расчете на 1 моль
поступающего в реактор метана. Полученное
уравнение, с учетом соотношения (16), позволяет
рассчитать требуемый поток теплоты для
достижения заданной степени конверсии метана
![]() 2,
меньшей или равной предельному равновесному
значению
2,
меньшей или равной предельному равновесному
значению ![]() 2 =
2 = ![]() 2,eq(
2,eq(![]() , Т2
), при любой комбинации параметров
, Т2
), при любой комбинации параметров ![]() , Т1 и Т2 .
, Т1 и Т2 .
В приближении постоянных теплоемкостей компонентов смеси справедливо выражение:
![]() rH(Т) =
rH(Т) = ![]() rH(298) +
rH(298) + ![]() rСp
(Т - 298) , (23)
rСp
(Т - 298) , (23)
где
![]() rH(298) =
rH(298) = ![]()
![]() H0f,i (298)
; (24)
H0f,i (298)
; (24)
![]() rСp =
rСp = ![]() Сp,i ; (25)
Сp,i ; (25)
![]() - стехиометрические
коэффициенты для рассматриваемой реакции (
- стехиометрические
коэффициенты для рассматриваемой реакции (![]() < 0 для исходных веществ
и
< 0 для исходных веществ
и ![]() > 0 для продуктов
реакции). В том же приближении разность энтальпий
для i-го вещества при температурах Т2 и
Т1 равна
> 0 для продуктов
реакции). В том же приближении разность энтальпий
для i-го вещества при температурах Т2 и
Т1 равна
Нi(Т2 ) - Нi(Т1) = Сp,i(Т2 - Т1) . (26)
Ясно, что для решения таких задач, как расчет требуемой для достижения конкретного значения x 2 длины реакционных труб при заданных условиях обогрева внешней поверхности труб, балансовых уравнений недостаточно. Для этих целей необходимо использование полноценной математической модели реактора в частных производных, включающей как кинетику химического превращения на гранулах катализатора, так и кинетику переноса теплоты через стенки реактора и в слое катализатора. Эти вопросы рассматриваются в последующей части курса.
Упражнения.
Таблица 2.Термодинамические данные
| Вещество |
СН4 |
Н2О (г) |
Н2 |
СО |
|
- 74848 |
- 241827 |
0 |
- 110525 |
С0P(298K) |
35.765 |
33.618 |
28.849 |
29.142 |
Вещество |
СО2 |
О2 |
N2 |
Ar |
|
- 393514 |
0 |
0 |
0 |
С0P(298K) |
37.220 |
29.370 |
29.125 |
20.785 |
| [предыдущий раздел] | [содержание] | [следующий раздел] |