|
Учебные материалы по физической химии
Реальные газы
Глава 1. Термодинамические свойства
реальных газов
Как известно, уравнение состояния
устанавливает функциональную связь между
давлением p, объемом V, температурой T и
числом молей n газа в состоянии равновесия.
Эта связь может выражаться не только в форме
уравнения, но также графически или в виде таблиц,
которые часто используются, особенно для
практических целей. Самым простым и известным
уравнением состояния является уравнение
состояния идеального газа:
pV = nRT (1.1)
где R – универсальная газовая постоянная.
Реальные газы описываются уравнением
состояния идеального газа только приближенно, и
отклонения от идеального поведения становятся
заметными при высоких давлениях и низких
температурах, особенно когда газ близок к
конденсации.
Так, для газов с низкой температурой сжижения
(He, H2, Ne и даже N2, O2, Ar, CO, CH4)
при давлениях до 50 атм отклонения не превышают 5%,
а при давлениях до 10 атм – 2%. Легко
конденсирующиеся газы (CO2, SO2, Cl2,
CH3Cl) уже при 1 атм обнаруживают отклонения
до 2 – 3%.
Одной из наглядных характеристик отклонений
реальных газов от идеального поведения
оказывается мольный объем газа Vm = V/n.
Для идеального газа он равен 22,414 л при 1 атм и 273 K.
Значения Vm для некоторых реальных
газов представлены в таблице 1.1.
Таблица 1.1. Мольные объемы газов при 1
атм и 273 K
| Газ |
Vm, л* моль-1 |
Газ |
Vm, л* моль-1 |
| H2 |
22,43 |
CO2 |
22,26 |
| He |
22,43 |
N2O |
22,25 |
| Ne |
22,42 |
H2O |
22,14 |
| F2 |
22,42 |
NH3 |
22,08 |
| N2 |
22,40 |
Cl2 |
22,02 |
| CO |
22,40 |
SO2 |
21,89 |
| O2 |
22,39 |
C4H10 |
21,50 |
| CH4 |
22,36 |
O3 |
21,60 |
Наиболее удобной мерой неидеальности является
фактор сжимаемости Z = pVm/RT,
поскольку для идеального газа Z = l при любых
условиях.
|
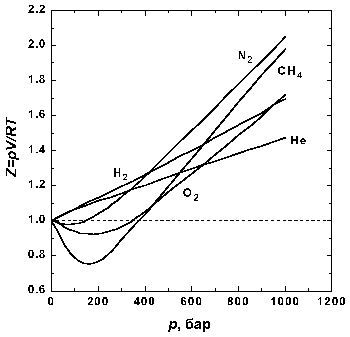
Рис.1.1 Зависимость фактора
сжимаемости некоторых газов от давления при 298 К. |
На рис. 1.1 представлены факторы сжимаемости для
некоторых реальных газов как функции давления
при 298 К (для сравнения поведение идеального газа
показано пунктиром). При высоких давлениях для
всех газов Z > 1, т.е. их труднее сжать, чем
идеальный газ, поскольку в этой области
преобладают силы межмолекулярного отталкивания.
Из рисунка видно, что при более низких давлениях
для некоторых газов Z < 1, что объясняется
преобладанием межмолекулярного притяжения. При p
 0 эффект
межмолекулярного притяжения исчезает, потому
что расстояние между молекулами стремится к
бесконечности, и для всех газов Z 0 эффект
межмолекулярного притяжения исчезает, потому
что расстояние между молекулами стремится к
бесконечности, и для всех газов Z  1, т.е. в этих условиях все газы ведут
себя почти идеально. 1, т.е. в этих условиях все газы ведут
себя почти идеально.
|
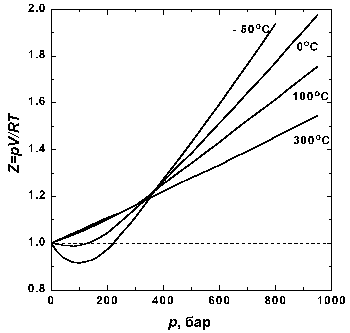
Рис1.2. Зависимость фактора
сжимаемости N2 от давления при разных
температурах. |
На рис. 1.2 представлены факторы сжимаемости для
азота при разных температурах. По мере
уменьшения температуры эффект межмолекулярного
притяжения увеличивается (что проявляется в
образовании минимума на кривых в области
давлений около 100 бар). Минимум на кривых
обнаруживается для всех газов, если
температура достаточно низка. У водорода и гелия,
имеющих очень низкие температуры кипения, этот
минимум наблюдается только при температурах
значительно ниже 0° C.
Из приведенных данных видно, что при низких
давлениях реальные газы могут быть более
сжимаемыми (Z < 1), чем идеальный газ, а при
высоких – менее (Z > 1). Очевидно, что
основными причинами отклонений свойств реальных
газов от свойств идеального газа оказываются
взаимное притяжение молекул и наличие у них
собственного объема. Наиболее ярко
межмолекулярное притяжение в реальных газах
проявляется в их способности к конденсации –
переходу в жидкое состояние.
1.1. Конденсация
Рассмотрим, что происходит, когда образец газа
в состоянии, отмеченном точкой А на рис. 1.3,
сжимается при постоянной температуре.
|
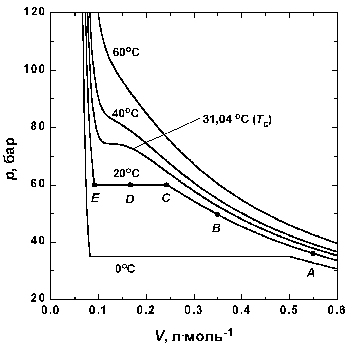
Рис 1.3. Экспериментальные
изотермы для СО2 |
Вблизи точки А давление возрастает
приблизительно по закону Бойля. Заметные
отклонения от закона Бойля начинают наблюдаться,
когда объем становится соизмеримым со значением,
указанным точкой В.
В точке С сходство с идеальным поведением
полностью теряется, так как оказывается, что
дальнейшее уменьшение объема не вызывает роста
давления; это показано горизонтальной линией CDE.
Исследование содержания сосуда показывает, что
сразу за точкой С появляется жидкость, и
можно наблюдать две фазы, разделенные резко
обозначенной границей – поверхностью раздела.
Поскольку при уменьшении объема газ
конденсируется, он не оказывает сопротивления
дальнейшему движению поршня. Давление,
соответствующее линии CDE, когда жидкость и
пар находятся в равновесии, называется давлением
пара жидкости при температуре опыта.
В точке Е весь образец представляет собой
жидкость, и дальнейшее уменьшение объема образца
требует значительного давления, поскольку
жидкости по сравнению с газами очень трудно
сжимаются, что проявляется в резком подъеме
кривой слева от точки Е.
1.2. Критические явления
Изотерма при температуре Tc играет
особую роль в теории состояния вещества.
Изотерма, соответствующая температуре ниже Tc,
ведет себя так, как уже описано: при определенном
давлении газ конденсируется в жидкость, которую
можно различать по наличию поверхности раздела.
Если же сжатие осуществлять при Tc, то
поверхность, разделяющая две фазы, не появляется,
а точка конденсации и точка полного перехода в
жидкость сливаются в одну критическую точку
газа. При температуре выше Tc газ
невозможно обратить в жидкость никаким сжатием.
Температура, давление и мольный объем в
критической точке называются критической
температурой Tc, критическим давлением pc
и критическим мольным объемом Vc
вещества. Собирательно параметры pc, Vc,
и Tc называются критическими
константами данного газа (таблица 1.2).
Таблица 1.2. Критические константы и
температуры Бойля
| Газ |
Tc, K |
Pc, бар |
Vc, мл* моль-1 |
Zc |
TB, K |
TB/Tc |
| He |
5,21 |
2,27 |
57,76 |
0,305 |
22,64 |
4,35 |
| Ne |
44,44 |
26,9 |
41,74 |
0,307 |
122,1 |
2,75 |
| Ar |
150,72 |
48,0 |
75,25 |
0,292 |
411,5 |
2,73 |
| Kr |
209,4 |
54,3 |
92,24 |
0,291 |
575,0 |
2,75 |
| Xe |
289,75 |
58,0 |
118,8 |
0,290 |
768,0 |
2,65 |
| H2 |
33,3 |
13,0 |
65,0 |
0,306 |
110,0 |
3,30 |
| N2 |
126,1 |
34,0 |
89,5 |
0,292 |
327,2 |
2,60 |
| O2 |
154,4 |
50,5 |
73,4 |
0,292 |
405,9 |
2,63 |
| CO2 |
304,2 |
73,8 |
94,0 |
0,274 |
714,8 |
2,35 |
| CH4 |
190,7 |
46,0 |
99,0 |
0,287 |
510,0 |
2,67 |
| C2H4 |
282,4 |
50,4 |
129,0 |
0,277 |
624 |
2,21 |
При T  Tc образец
представляет собой фазу, полностью занимающую
объем содержащего ее сосуда, т. е. по определению
является газом. Однако плотность этой фазы может
быть значительно большей, чем это типично для
газов, поэтому обычно предпочитают название "сверхкритический
флюид" (supercritical fluid). Tc образец
представляет собой фазу, полностью занимающую
объем содержащего ее сосуда, т. е. по определению
является газом. Однако плотность этой фазы может
быть значительно большей, чем это типично для
газов, поэтому обычно предпочитают название "сверхкритический
флюид" (supercritical fluid).
В критической точке изотермический
коэффициент сжимаемости 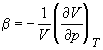 равен бесконечности, поскольку равен бесконечности, поскольку 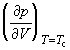 = 0. Поэтому вблизи
критической точки сжимаемость вещества так
велика, что ускорение силы тяжести приводит к
значительным различиям плотности в верхней и
нижней частях сосуда, достигающим 10% в столбике
вещества высотой всего несколько сантиметров.
Это затрудняет определение плотностей (удельных
объемов) и, соответственно, изотерм p – V
вблизи критической точки. В то же время
критическую температуру можно определить весьма
точно как такую температуру, при которой
поверхность, разделяющая газообразную и жидкую
фазы, исчезает при нагревании и вновь появляется
при охлаждении. Зная критическую температуру,
можно определить критическую плотность (и,
соответственно, критический мольный объем),
пользуясь эмпирическим правилом прямолинейного
диаметра (правило Кальете-Матиаса), согласно
которому средняя плотность жидкости и
насыщенного пара является линейной функцией
температуры: = 0. Поэтому вблизи
критической точки сжимаемость вещества так
велика, что ускорение силы тяжести приводит к
значительным различиям плотности в верхней и
нижней частях сосуда, достигающим 10% в столбике
вещества высотой всего несколько сантиметров.
Это затрудняет определение плотностей (удельных
объемов) и, соответственно, изотерм p – V
вблизи критической точки. В то же время
критическую температуру можно определить весьма
точно как такую температуру, при которой
поверхность, разделяющая газообразную и жидкую
фазы, исчезает при нагревании и вновь появляется
при охлаждении. Зная критическую температуру,
можно определить критическую плотность (и,
соответственно, критический мольный объем),
пользуясь эмпирическим правилом прямолинейного
диаметра (правило Кальете-Матиаса), согласно
которому средняя плотность жидкости и
насыщенного пара является линейной функцией
температуры:
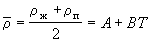 , (1.2) , (1.2)
где A и B – постоянные для данного
вещества величины. Экстраполируя прямую средней
плотности 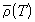 до
критической температуры, можно определить
критическую плотность (см. задачу 1.7). до
критической температуры, можно определить
критическую плотность (см. задачу 1.7).
Высокая сжимаемость вещества вблизи
критической точки приводит к росту спонтанных
флуктуаций плотности, которые сопровождаются
аномальным рассеянием света. Это явление
называется критической опалесценцией.
|

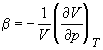 равен бесконечности, поскольку
равен бесконечности, поскольку 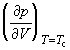 = 0. Поэтому вблизи
критической точки сжимаемость вещества так
велика, что ускорение силы тяжести приводит к
значительным различиям плотности в верхней и
нижней частях сосуда, достигающим 10% в столбике
вещества высотой всего несколько сантиметров.
Это затрудняет определение плотностей (удельных
объемов) и, соответственно, изотерм p – V
вблизи критической точки. В то же время
критическую температуру можно определить весьма
точно как такую температуру, при которой
поверхность, разделяющая газообразную и жидкую
фазы, исчезает при нагревании и вновь появляется
при охлаждении. Зная критическую температуру,
можно определить критическую плотность (и,
соответственно, критический мольный объем),
пользуясь эмпирическим правилом прямолинейного
диаметра (правило Кальете-Матиаса), согласно
которому средняя плотность жидкости и
насыщенного пара является линейной функцией
температуры:
= 0. Поэтому вблизи
критической точки сжимаемость вещества так
велика, что ускорение силы тяжести приводит к
значительным различиям плотности в верхней и
нижней частях сосуда, достигающим 10% в столбике
вещества высотой всего несколько сантиметров.
Это затрудняет определение плотностей (удельных
объемов) и, соответственно, изотерм p – V
вблизи критической точки. В то же время
критическую температуру можно определить весьма
точно как такую температуру, при которой
поверхность, разделяющая газообразную и жидкую
фазы, исчезает при нагревании и вновь появляется
при охлаждении. Зная критическую температуру,
можно определить критическую плотность (и,
соответственно, критический мольный объем),
пользуясь эмпирическим правилом прямолинейного
диаметра (правило Кальете-Матиаса), согласно
которому средняя плотность жидкости и
насыщенного пара является линейной функцией
температуры: