4.2.3. Выражение работоспособности системы через функцию эксергия
Интегральные уравнения баланса потоков энергии и энтропии (3.9) и (4.10) в
совокупности с определением полной работы системы (4.7) составляют основу для
постановки и решения центрального вопроса данного раздела курса – о
существовании и определении тех траекторий процесса преобразования
материального потока, которые обеспечивают максимальную величину полной работы
системы.
В уравнении полной работы (4.7) потоки 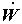 и и 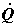 необходимо выразить через термодинамические
функции состояния. Для этого разность необходимо выразить через термодинамические
функции состояния. Для этого разность 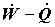 определим из уравнения баланса энергии
(3.9), а приведенный поток теплоты определим из уравнения баланса энергии
(3.9), а приведенный поток теплоты 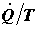 – из уравнения баланса энтропии (4.10). В
итоге найдем – из уравнения баланса энтропии (4.10). В
итоге найдем
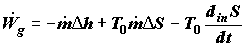 . (4.13) . (4.13)
Вводя функцию 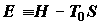 , называемую эксергией , и ее удельную величину , называемую эксергией , и ее удельную величину 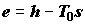 , представим
выражение (4.13) в форме , представим
выражение (4.13) в форме
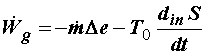 , (4.14) , (4.14)
где 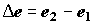 ; e1
и e2 – удельные эксергии на входе и выходе материального
потока. ; e1
и e2 – удельные эксергии на входе и выходе материального
потока.
Прежде всего убеждаемся, что полученное выражение не зависит от сложности
описания процессов теплообмена системы с внешним окружением. Действительно, в
том случае, когда участвующие в теплообмене части системы имеют разную
температуру, основываясь на расширенном определении полной работы (4.9) и
определяя сумму приведенных теплот из уравнения баланса энтропии (4.11),
приходим к той же формуле (4.13).
При дифференцированном описании всех входов и выходов из системы, исходя из
уравнений баланса энергии и энтропии в форме (3.10) и (4.12), получим выражение
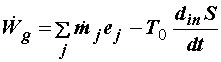 , (4.15) , (4.15)
в котором ej – удельная эксергия j
-го материального потока.
Полученные выражения (4.14) и (4.15) дают полный ответ на сформулированный
выше вопрос. Согласно второму закону термодинамики 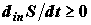 , причем производство энтропии
равно нулю, если и только если в системе не совершаются неравновесные процессы.
Таким образом, выражения (4.14) и (4.15) устанавливают, что при заданном
преобразовании , причем производство энтропии
равно нулю, если и только если в системе не совершаются неравновесные процессы.
Таким образом, выражения (4.14) и (4.15) устанавливают, что при заданном
преобразовании 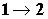 совокупного материального потока через систему существуют
такие траектории этого преобразования, при которых полная работа системы
максимальна, и таковыми траекториями являются равновесные траектории перевода
вещества из начального состояния "1" в конечное состояние "1".
Множество равновесных траекторий (эквивалентных с точки зрения
термодинамической эффективности) может быть бесконечным. совокупного материального потока через систему существуют
такие траектории этого преобразования, при которых полная работа системы
максимальна, и таковыми траекториями являются равновесные траектории перевода
вещества из начального состояния "1" в конечное состояние "1".
Множество равновесных траекторий (эквивалентных с точки зрения
термодинамической эффективности) может быть бесконечным.
Более того, уравнения (4.14) и (4.15) вполне конструктивны в том смысле, что
определяют саму величину максимальной работы, выражая ее через изменения
энтальпии и энтропии рабочих веществ, рассчитываемые стандартными
термодинамическими методами:
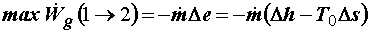 , (4.16) , (4.16)
или
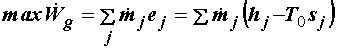 . (4.17) . (4.17)
Максимальная полная работа положительна, если в системе эксергия совокупного
материального потока падает, 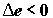 , и отрицательна, если эксергия потока возрастает, , и отрицательна, если эксергия потока возрастает, 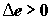 . В последнем
случае, очевидно, . В последнем
случае, очевидно, 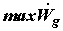 соответствует минимуму абсолютной величины полной работы,
т.е. минимуму затрат полной работы. соответствует минимуму абсолютной величины полной работы,
т.е. минимуму затрат полной работы.
Максимальное значение полной работы характеризует гипотетическую
потенциальную возможность получения квалифицированной формы энергии в ходе
данной трансформации вещества 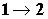 . Гипотетической эта возможность является как в силу гипотезы
квазиравновесности внутрисистемных процессов, так и в силу предположения о
квазиравновесности циклических процессов преобразования отводимой от системы
теплоты в работу (или работы в подводимую к системе теплоту) в идеальной машине
Карно. Тем не менее, знание этого предельного значения очень важно с той точки
зрения, что позволяет количественно охарактеризовать степень термодинамического
несовершенства любой реальной (или проектируемой) технологической системы и тем
самым оценить имеющиеся резервы в повышении эффективности использования
энергоресурсов. . Гипотетической эта возможность является как в силу гипотезы
квазиравновесности внутрисистемных процессов, так и в силу предположения о
квазиравновесности циклических процессов преобразования отводимой от системы
теплоты в работу (или работы в подводимую к системе теплоту) в идеальной машине
Карно. Тем не менее, знание этого предельного значения очень важно с той точки
зрения, что позволяет количественно охарактеризовать степень термодинамического
несовершенства любой реальной (или проектируемой) технологической системы и тем
самым оценить имеющиеся резервы в повышении эффективности использования
энергоресурсов.
В любом реальном технологическом процессе 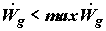 , т.е. эксергия материального потока
используется не полностью. По аналогии с функцией возникновения (производства)
энтропии может быть введена функция исчезновения (потерь) эксергии в
неравновесном процессе, характеризующая разность между максимальным и реальным
значением полной работы в системе: , т.е. эксергия материального потока
используется не полностью. По аналогии с функцией возникновения (производства)
энтропии может быть введена функция исчезновения (потерь) эксергии в
неравновесном процессе, характеризующая разность между максимальным и реальным
значением полной работы в системе:
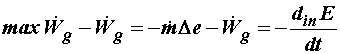 , (4.18) , (4.18)
или
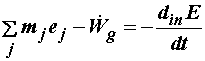 , (4.19) , (4.19)
где 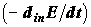 –
скорость внутрисистемной диссипации эксергии. Поскольку H и S
являются экстенсивными термодинамическими функциями, то образованная из них
функция E также выражает экстенсивное, т.е. пропорциональное
массе, свойство системы (собственно на этом основано использование функции
удельной эксергии e). Поэтому уравнения (4.18) и (4.19)
могут считаться уравнениями баланса эксергии в технологической системе. –
скорость внутрисистемной диссипации эксергии. Поскольку H и S
являются экстенсивными термодинамическими функциями, то образованная из них
функция E также выражает экстенсивное, т.е. пропорциональное
массе, свойство системы (собственно на этом основано использование функции
удельной эксергии e). Поэтому уравнения (4.18) и (4.19)
могут считаться уравнениями баланса эксергии в технологической системе.
Сопоставляя уравнения (4.14) и (4.18), или соответственно (4.15) и (4.19),
находим
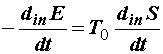 . (4.20) . (4.20)
Последнее соотношение по существу является связующим мостом между теорией
энергосберегающих технологий и термодинамикой необратимых процессов.
Материал данного раздела необходимо дополнить следующими замечаниями.
1. Выражение полной работы (4.13) основано на "сокращенном"
уравнении баланса потоков энергии (3.9). Если вернуться к первоначальному
уравнению сохранения энергии (3.8), учитывающему также изменение кинетической и
потенциальной энергии рабочего вещества, то придем к расширенному определению
удельной эксергии
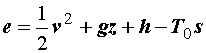 , (4.21) , (4.21)
которое может быть использовано во всех выписанных выше уравнениях баланса
эксергии. На соотношении (4.20) такое расширенное толкование не отражается.
2. Сопоставим между собой термодинамические потенциалы 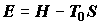 и и 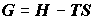 . Функция Гиббса
определяет максимальную "чистую" работу системы в изотермическом
процессе ( T = const): . Функция Гиббса
определяет максимальную "чистую" работу системы в изотермическом
процессе ( T = const):
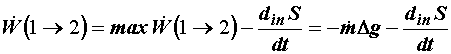 , ,
где 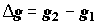 ; g1
и g2 – удельные значения функции Гиббса на входе и выходе
системы. Введение функции эксергии, во-первых, позволяет учесть потенциальную
возможность преобразования в работу отводимой от системы теплоты
(характеризуемую слагаемым ; g1
и g2 – удельные значения функции Гиббса на входе и выходе
системы. Введение функции эксергии, во-первых, позволяет учесть потенциальную
возможность преобразования в работу отводимой от системы теплоты
(характеризуемую слагаемым 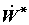 ) и во-вторых, и это главное, расширяет возможности
термодинамического анализа применительно к неизотермическим процессам,
наиболее распространенным в технологии. Очевидно, обе функции тождественны при T
= To. ) и во-вторых, и это главное, расширяет возможности
термодинамического анализа применительно к неизотермическим процессам,
наиболее распространенным в технологии. Очевидно, обе функции тождественны при T
= To.
3. Температура универсального теплового резервуара To
, фигурирующая в определениях полной работы и функции эксергии, вообще говоря,
не является постоянным параметром. Принимаемые значения To
должны отражать региональную специфику окружающей среды в географической точке
расположения конкретного производства, сезонные и, возможно, даже суточные
температурные колебания той части природной среды (воздушный бассейн,
прибрежные воды океана и т.д.), которая используется в качестве внешнего
источника или стока теплоты. И из повседневного опыта известно, например, что отдача
топливного двигателя в морозную погоду ощутимо выше, чем в жаркие дни. Однако в
целом для оценки термодинамической эффективности разнообразных технологических
систем девиации температуры To имеют второстепенное
значение, в особенности при анализе наиболее энергонасыщенных,
высокотемпературных или низкотемпературных процессов (когда перепады
температуры 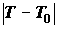 много больше колебаний To).
В теоретических расчетах удобнее всего положить To
равным условной стандартной температуре 298 К, для которой в справочниках
приводятся необходимые значения энтальпии и энтропии веществ. много больше колебаний To).
В теоретических расчетах удобнее всего положить To
равным условной стандартной температуре 298 К, для которой в справочниках
приводятся необходимые значения энтальпии и энтропии веществ.
|

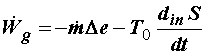 , (4.14)
, (4.14)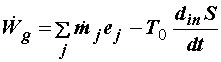 , (4.15)
, (4.15)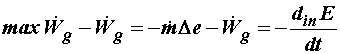 , (4.18)
, (4.18)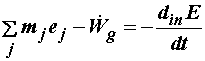 , (4.19)
, (4.19)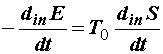 . (4.20)
. (4.20)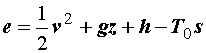 , (4.21)
, (4.21)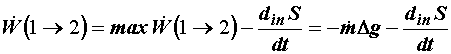 ,
,