4.1.2. Цикл Карно
Предельные соотношения для перехода теплоты в работу вытекают из анализа
циклического процесса, совершаемого тепловой машиной Карно. В этом процессе
каждая индивидуальная порция рабочего вещества претерпевает последовательное
четырехстадийное изменение состояния: изотермическое расширение с получением
теплоты 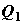 от
теплового резервуара – источника теплоты при температуре T1;
адиабатическое расширение, сопровождаемое охлаждением до температурыT2;
изотермическое сжатие с отводом теплоты от
теплового резервуара – источника теплоты при температуре T1;
адиабатическое расширение, сопровождаемое охлаждением до температурыT2;
изотермическое сжатие с отводом теплоты 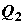 к тепловому резервуару – стоку теплоты
при температуре T2 и адиабатическое сжатие,
сопровождаемое нагреванием до первоначальной температуры T1.
Суммарная работа, совершаемая выделенной порцией рабочего вещества (таковым
может быть, например, индивидуальный газ, газовая смесь, гетерогенная смесь
жидкость-пар), за один цикл равна к тепловому резервуару – стоку теплоты
при температуре T2 и адиабатическое сжатие,
сопровождаемое нагреванием до первоначальной температуры T1.
Суммарная работа, совершаемая выделенной порцией рабочего вещества (таковым
может быть, например, индивидуальный газ, газовая смесь, гетерогенная смесь
жидкость-пар), за один цикл равна
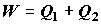 , (4.1) , (4.1)
где 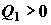 и и 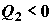 ; знаки потоков
теплоты выбраны относительно тепловой машины как исследуемой системы. ; знаки потоков
теплоты выбраны относительно тепловой машины как исследуемой системы.
В идеальной тепловой машине Карно все процессы протекают
квазиравновесно и, кроме того, теплоперенос от источника к рабочему веществу и
от рабочего вещества к стоку теплоты также происходит квазиравновесно
(температура рабочего вещества на неадиабатических стадиях поддерживается
близкой к температуре теплового резервуара); в этом предположении в
соответствии с "равновесной" частью формулировки второго закона
(2.1), при полном обходе замкнутой траектории изменения состояния рабочего
вещества имеем уравнение сохранения энтропии
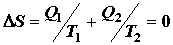 . (4.2) . (4.2)
Исключая 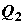 из уравнений (4.1) и (4.2), получаем из уравнений (4.1) и (4.2), получаем
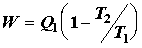 . (4.3) . (4.3)
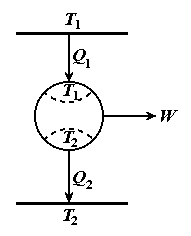
Рис. 4.1. Схема тепловой машины
Карно (по Р.Хейвуду).
На рис. 4.1 приведена выразительная схема тепловой машины Карно,
использованная в книге Р.Хейвуда "Термодинамика равновесных
процессов". Траектория изменения состояния рабочего вещества в цикле
наиболее простую форму приобретает на плоскости параметров S-T
(рис.4.2). Работа цикла равна площади прямоугольника, изображающего эту
траекторию. Ключевым моментом для замыкания траектории является остановка
стадии изотермического сжатия в точке S = S1.
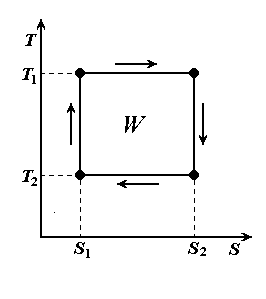
Рис. 4.2. Траектория изменения
состояния рабочего вещества в цикле Карно.
Формула (4.3) показывает, что необходимым условием производства работы
тепловой машины 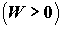 является перенос теплоты от "горячего" к
"холодному" резервуару, является перенос теплоты от "горячего" к
"холодному" резервуару, 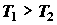 . Степень преобразования подведенной к
машине теплоты в работу характеризуется коэффициентом полезного действия . Степень преобразования подведенной к
машине теплоты в работу характеризуется коэффициентом полезного действия
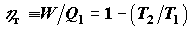 . (4.4) . (4.4)
Если циклический процесс в машине Карно не идеален, т.е. включает какие-либо
неравновесные процессы, то вместо равенства (4.2) имеет место неравенство 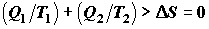 , откуда , откуда
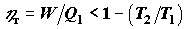 . .
Особая роль, которую играет в термодинамике равновесный цикл Карно,
определяется тем обстоятельством, что в этом цикле достигается максимальный
к.п.д. тепловой машины по сравнению с любыми другими циклическими процессами в
том же диапазоне рабочих температур (T2,T1)
.
Приведем вариант доказательства этого важного утверждения, не используя
никаких дополнительных предложений помимо исходной формулировки второго закона
(2.1). В произвольном циклическом процессе всегда можно выделить совокупность
элементарных тепловых источников 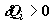 , подводящих теплоту при соответствующих
локальных температурах Tj, и совокупность
элементарных стоков теплоты , подводящих теплоту при соответствующих
локальных температурах Tj, и совокупность
элементарных стоков теплоты 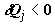 , отводящих теплоту при температурах Tj.
Работу цикла можно представить тогда как , отводящих теплоту при температурах Tj.
Работу цикла можно представить тогда как
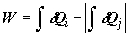 ; ;
к.п.д. цикла равен
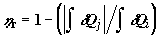 . .
Неравенство (2.1) в применении к рассматриваемому процессу примет форму
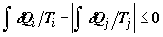 . .
Поскольку цикл не совпадает с циклом Карно, то 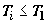 и и 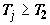 , причем хотя бы для отдельных
элементарных источников или стоков выполняются именно неравенства. Тогда , причем хотя бы для отдельных
элементарных источников или стоков выполняются именно неравенства. Тогда
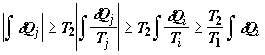 , ,
причем хотя бы одно из трех неравенств выполняется строго (иначе цикл
тождествен равновесному циклу Карно). Отсюда следует
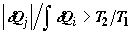 и и 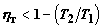 . .
По ходу этого доказательства становится очевидной причина экстремальной
эффективности цикла Карно: в этом цикле вся потребляемая теплота имеет наиболее
высокий потенциал, а вся отводимая теплота – наиболее низкий потенциал в
заданных границах температурного интервала.
Машина Карно может быть запущена и в обратном направлении; все стадии
циклического процесса при этом изменятся на противоположно направленные. На
рис. 4.2 этому будет соответствовать обход той же самой равновесной траектории
против часовой стрелки. Уравнения (4.1) – (4.4) остаются справедливыми и для
такого варианта функционирования машины Карно, но величины, характеризующие
потоки энергии, изменяют свои знаки на противоположные: 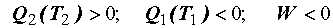 . Машина Карно будет
переносить теплоту с нижнего температурного уровня T2
на более высокий температурный уровень T1, не
производя, а затрачивая работу. Можно доказать, по аналогии с предыдущим, что
обратный идеальный цикл Карно обеспечивает минимальные затраты работы по
сравнению с любыми другими циклическими процессами при перекачке заданного количества
теплоты из резервуаров с температурой . Машина Карно будет
переносить теплоту с нижнего температурного уровня T2
на более высокий температурный уровень T1, не
производя, а затрачивая работу. Можно доказать, по аналогии с предыдущим, что
обратный идеальный цикл Карно обеспечивает минимальные затраты работы по
сравнению с любыми другими циклическими процессами при перекачке заданного количества
теплоты из резервуаров с температурой 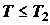 в резервуары с температурой в резервуары с температурой 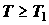 . .
|



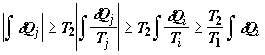 ,
,