|
Учебные материалы по неорганической химии
Правило фаз (однокомпонентные системы)
Глава 2.Правило фаз для
однокомпонентной системы
Для однокомпонентной системы (К=1) правило фаз
записывается в виде
С = 3-Ф . (9)
Если Ф = 1, то С =2 , говорят, что система бивариантна;
Ф = 2, то С =1 , система моновариантна;
Ф = 3, то С =0 , система нонвариантна.
Соотношение между давлением (р), температурой
(Т) и объемом (V) фазы можно представить трехмерной
фазовой диаграммой. Каждая точка (ее называют
фигуративной точкой) на такой диаграмме
изображает некоторое равновесное состояние.
Обычно удобнее работать с сечениями этой
диаграммы плоскостью р - Т (при V=const) или
плоскостью р -V (при T=const). Разберем более детально
случай сечения плоскостью р - Т (при V=const).
2.1. Фазовая диаграмма воды
Фазовая диаграмма воды в координатах р - Т
представлена на рис.1. Она составлена из 3 фазовых
полей - областей различных (р,Т)-значений, при
которых вода существует в виде определенной фазы
- льда, жидкой воды или пара ( обозначены на рис.1
буквами Л, Ж и П, соответственно). Эти фазовые поля
разделены 3 граничными кривыми.
Кривая АВ - кривая испарения, выражает
зависимость давления пара жидкой воды от
температуры (или, наоборот, представляет
зависимость температуры кипения воды от
давления). Другими словами, эта линия отвечает двухфазному
равновесию (жидкая вода) D (пар), и число
степеней свободы, рассчитанное по правилу фаз,
составляет С = 3 - 2 = 1. Такое равновесие называют
моновариантным. Это означает, что для полного
описания системы достаточно определить только одну
переменную - либо температуру, либо давление,
т.к. для данной температуры существует только
одно равновесное давление и для данного давления
- только одна равновесная температура.
При давлениях и температурах, соответствующих
точкам ниже линии АВ, жидкость будет полностью
испаряться, и эта область является областью пара.
Для описания системы в данной однофазной
области необходимы две независимые
переменные (С = 3 - 1 = 2): температура и давление.
При давлениях и температурах, соответствующих
точкам выше линии АВ, пар полностью
сконденсирован в жидкость (С = 2). Верхний предел
кривой испарения AB находится в точке В, которая
называется критической точкой (для воды 374o
С и 218 атм). Выше этой температуры фазы жидкости и
пара становятся неразличимыми (исчезает четкая
межфазная граница жидкость/пар), поэтому Ф=1.
Линия АС - эта кривая возгонки льда
(иногда ее называют линией сублимации),
отражающая зависимость давления водяного пара
надо льдом от температуры. Эта линия
соответствует моновариантному равновесию
(лед) D (пар) (С=1). Выше линии АС лежит область льда,
ниже - область пара.
Линия АD -кривая плавления, выражает
зависимость температуры плавления льда от
давления и соответствует моновариантному
равновесию (лед) D (жидкая вода). Для большинства
веществ линия АD отклоняется от вертикали вправо,
но поведение воды
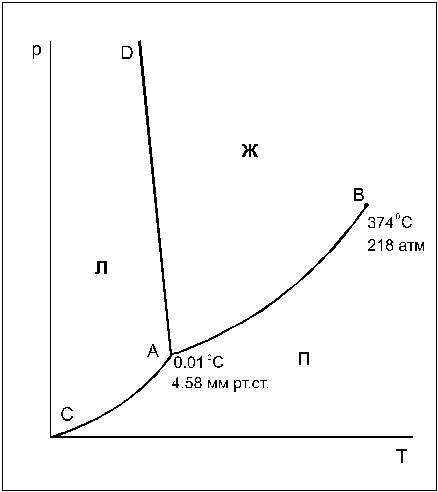
Рис.1. Фазовая диаграмма воды
аномально: жидкая вода занимает меньший
объем, чем лед. На основании принципа Ле
Шателье можно предсказать, что повышение
давления будет вызывать сдвиг равновесия в
сторону образования жидкости, т.е. точка
замерзания будет понижаться.
Исследования, проведенные Бриджменом для
определения хода кривой плавления льда при
высоких давлениях, показали, что существует семь
различных кристаллических модификаций льда,
каждая из которых, за исключением первой, плотнее
воды. Таким образом, верхний предел линии AD -
точка D, где в равновесии находятся лед I (обычный
лед), лед III и жидкая вода. Эта точка находится при
-220С и 2450 атм (см.задачу 11).
Тройная точка воды (точка , отражающая
равновесие трех фаз - жидкости, льда и пара) в
отсутствие воздуха находится при 0,0100o С и
4,58 мм рт.ст. Число степеней свободы С=3-3=0 и такое
равновесие называют нонвариантным.
В присутствии воздуха три фазы находятся в
равновесии при 1 атм и при 0o С. Понижение
тройной точки на воздухе вызвано следующим
причинами:
1. растворимостью воздуха в жидкой воде при 1 атм,
что приводит к снижению тройной точки на 0,0024o
С;
2. увеличением давления от 4,58 мм рт.ст. до 1 атм,
которое снижает тройную точку еще на 0.0075o С.
2.2. Фазовая диаграмма серы
Кристаллическая сера существует в виде двух
модификаций – ромбической (Sр) и моноклинной
(Sм). Поэтому возможно существование
четырех фаз: ромбической, моноклинной, жидкой и
газообразной (рис.2). Сплошные линии ограничивают
четыре области: пара, жидкости и двух
кристаллических модификаций. Сами линии
отвечают моновариантным равновесиям двух
соответствующих фаз. Заметьте, что линия
равновесия моноклинная сера - расплав отклонена
от вертикали вправо ( сравните с фазовой
диаграммой воды ). Это означает, что при
кристаллизации серы из расплава происходит
уменьшение объема. В точках А, В и С в
равновесии сосуществуют 3 фазы (точка А –
ромбическая, моноклинная и пар, точка В –
ромбическая, моноклинная и жидкость, точка С –
моноклинная, жидкость и пар). Легко заметить, что
есть еще одна точка О,
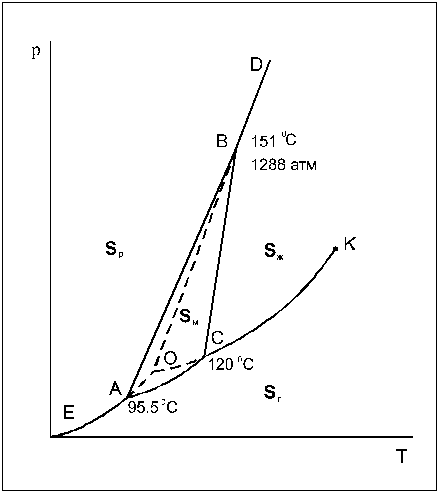
Рис.2. Фазовая диаграмма серы
в которой существует равновесие трех фаз –
перегретой ромбической серы, переохлажденной
жидкой серы и пара, пересыщенного относительно
пара, равновесного с моноклинной серой. Эти три
фазы образуют метастабильную систему, т.е.
систему, находящуюся в состоянии относительной
устойчивости. Кинетика превращения
метастабильных фаз в термодинамически
стабильную модификацию крайне медленна, однако
при длительной выдержке или внесении
кристаллов-затравок моноклинной серы все три
фазы все же переходят в моноклинную серу, которая
является термодинамически устойчивой в
условиях, отвечающих точке О. Равновесия, которым
соответствуют кривые ОА, ОВ и ОС (кривые –
возгонки, плавления и испарения, соответственно)
являются метастабильными.
В случае диаграммы серы мы сталкиваемся с
самопроизвольным взаимным превращением двух
кристаллических модификаций, которые могут
протекать в прямом и обратном направлении в
зависимости от условий. Такого типа превращения
называются энантиотропными (обратимыми).
Взаимные превращения кристаллических фаз,
которые могут протекать лишь в одном
направлении, называются монотропными (необратимыми).
Примером монотропного превращения является
переход белого фосфора в фиолетовый.
2.3. Уравнение Клаузиуса - Клапейрона
Движение вдоль линий двухфазного равновесия на
фазовой диаграмме ( С=1 ) означает согласованное
изменение давления и температуры, т.е. р=f(Т). Общий
вид такой функции для однокомпонентных систем
был установлен Клапейроном.
Допустим, мы имеем моновариантное равновесие
(вода) D (лед) (линия AD на рис.1 ). Условие равновесия
будет выглядеть так : для любой точки с
координатами (р,Т), принадлежащей линии AD,  воды(р,Т) = воды(р,Т) =  льда(р,Т).
Для однокомпонентной системы льда(р,Т).
Для однокомпонентной системы  =G/n,
где G - свободная энергия Гиббса, а n - число молей
(=const). Нужно выразить =G/n,
где G - свободная энергия Гиббса, а n - число молей
(=const). Нужно выразить  G=f(p,T).
Формула G=f(p,T).
Формула  G= G= H-T H-T S для этой цели не годится, т.к.
выведена для р,Т=const. В общем виде, Gє H-TS=U+pV-TS.
Найдем дифференциал dG, используя правила для
дифференциала суммы и произведения: dG=dU+p.
dV+V. dp-T. dS-S. dT. Согласно 1-му
закону термодинамики dU=dQ - dA, причем dQ=T. dS,a dA=
p. dV. Тогда dG=V. dp - S. dT. Очевидно,
что в равновесии dGводы/n=dGльда/n (n=nводы=nльда=сonst).
Тогда vводы. dp-sводы. dT=vльда.
dp-sльда. dT, где vводы, vльда
- мольные (т.е. деленные на количество молей)
объемы воды и льда, sводы, sльда -
мольные энтропии воды и льда. Преобразуем
полученное выражение в (vводы - vльда).
dp = (sводы - sльда). dT, (10) S для этой цели не годится, т.к.
выведена для р,Т=const. В общем виде, Gє H-TS=U+pV-TS.
Найдем дифференциал dG, используя правила для
дифференциала суммы и произведения: dG=dU+p.
dV+V. dp-T. dS-S. dT. Согласно 1-му
закону термодинамики dU=dQ - dA, причем dQ=T. dS,a dA=
p. dV. Тогда dG=V. dp - S. dT. Очевидно,
что в равновесии dGводы/n=dGльда/n (n=nводы=nльда=сonst).
Тогда vводы. dp-sводы. dT=vльда.
dp-sльда. dT, где vводы, vльда
- мольные (т.е. деленные на количество молей)
объемы воды и льда, sводы, sльда -
мольные энтропии воды и льда. Преобразуем
полученное выражение в (vводы - vльда).
dp = (sводы - sльда). dT, (10)
или: dp/dT= sфп/ sфп/ vфп , (11) vфп , (11)
где  sфп, sфп,  vфп - изменения мольных
энтропии и объема при фазовом переходе ((лед) vфп - изменения мольных
энтропии и объема при фазовом переходе ((лед) (вода) в
данном случае). (вода) в
данном случае).
Поскольку  sфп = sфп =  H фп/Тфп, то чаще
применяют следующий вид уравнения: H фп/Тфп, то чаще
применяют следующий вид уравнения:

где  Hфп - изменения
энтальпии при фазовом переходе, Hфп - изменения
энтальпии при фазовом переходе,
 vфп - изменение мольного
объема при переходе, vфп - изменение мольного
объема при переходе,
Тфп - температура при которой происходит
переход.
Уравнение Клапейрона позволяет, в частности,
ответить на следующий вопрос: какова
зависимость температуры фазового перехода от
давления? Давление может быть внешним или
создаваться за счет испарения вещества.
Пример 6. Известно, что лед имеет больший
мольный объем, чем жидкая вода. Тогда при
замерзании воды  vфп = vльда
- vводы > 0, в то же время vфп = vльда
- vводы > 0, в то же время  Hфп
= Hфп
=  Hкрист < 0, поскольку
кристаллизация всегда сопровождается
выделением теплоты. Следовательно, Hкрист < 0, поскольку
кристаллизация всегда сопровождается
выделением теплоты. Следовательно,  Hфп/(T. Hфп/(T.  vфп)< 0 и, согласно
уравнению Клапейрона, производная dp/dT< 0. Это
означает, что линия моновариантного равновесия
(лед) D (вода) на фазовой диаграмме воды должна
образовывать тупой угол с осью температур. vфп)< 0 и, согласно
уравнению Клапейрона, производная dp/dT< 0. Это
означает, что линия моновариантного равновесия
(лед) D (вода) на фазовой диаграмме воды должна
образовывать тупой угол с осью температур.
Пример 7. Отрицательное значение dp/dT для
фазового перехода (лед) " (вода) означает, что
под давлением лед может плавится при температуре
ниже 0 0С. Основываясь на этой
закономерности, английские физики Тиндаль и
Рейнольдс около 100 лет назад предположили, что
известная легкость скольжения по льду на коньках
связана с плавлением льда под острием конька;
образующаяся при этом жидкая вода действует как
смазка. Проверим, так ли это, используя уравнение
Клапейрона.
Плотность воды -  в = 1 г/см3,
плотность льда - в = 1 г/см3,
плотность льда -  л = 1.091 г/см3,
молекулярная масса воды - М = 18 г/моль. Тогда: л = 1.091 г/см3,
молекулярная масса воды - М = 18 г/моль. Тогда:
 vфп = М/ vфп = М/ в-М/ в-М/ л = 18/1.091-18/1= -1.501 см3/моль
= -1.501. 10-6 м3/моль, л = 18/1.091-18/1= -1.501 см3/моль
= -1.501. 10-6 м3/моль,
энтальпия плавления льда -  Нфп
= 6.009 кДж/моль, Нфп
= 6.009 кДж/моль,
Тфп = 00С=273 К.
По уравнению Клапейрона:
dp/dT= - (6.009. 103 Дж/моль)/(273К. 1.501.
10-6м3/моль)=
= - 146.6. 105 Па/К= -146 атм/К.
Значит, для плавления льда при температуре,
скажем, -100С необходимо приложить давление
1460 атм. Но такой нагрузки лед не выдержит!
Следовательно, изложенная выше идея не
соответствует действительности. Реальная же
причина плавления льда под коньком - теплота,
выделяемая при трении.
Клаузиус упростил уравнение Клапейрона в
случае испарения и возгонки, предположив,
что:
- пар подчиняется закону идеального газа,
- мольный объем жидкости vж (или vтв)
<< vпара.
Подставим  vфп vфп  vпара = RT/p (из газовых законов)
в уравнение Клапейрона: vпара = RT/p (из газовых законов)
в уравнение Клапейрона:
dp/dT=(p.  Hисп)/(R.
T2), (12) Hисп)/(R.
T2), (12)
разделяя переменные получим:
dp/p=( Hисп/R). (dT/T2).
(13) Hисп/R). (dT/T2).
(13)
Проинтегрируем левую часть в пределах от р1
до р2, а правую - от Т1 до Т2 (т.е.
от одной точки (р1,Т1), лежащей на линии
равновесия (жидкость) D (пар), до другой - (р2,Т2)):
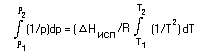 (14) (14)
Результат интгерирования запишем в виде:
ln р2 - ln р1 =  Hисп/R.
(1/T1 - 1/T2) , (15) Hисп/R.
(1/T1 - 1/T2) , (15)
называемым иногда уравнением
Клаузиуса-Клапейрона. Оно может быть
использовано для расчета теплоты испарения или
возгонки, если известны значения давлений пара
при двух различных температурах.
2.4. Энтропия испарения
Мольная энтропия испарения  Sисп =
Sисп =  Hисп/Ткип
равна разности Sпара - Sжидк.
Поскольку Sпара >> Sжидк, то можно
полагать Hисп/Ткип
равна разности Sпара - Sжидк.
Поскольку Sпара >> Sжидк, то можно
полагать  Sисп Sисп  Sпара. Следующее допущение
состоит в том, что пар считают идеальным газом.
Отсюда вытекает приблизительное постоянство
мольной энтропии испарения жидкости при
температуре кипения, называемое правилом
Трутона. Sпара. Следующее допущение
состоит в том, что пар считают идеальным газом.
Отсюда вытекает приблизительное постоянство
мольной энтропии испарения жидкости при
температуре кипения, называемое правилом
Трутона.
Правило Трутона. Мольная энтропия
испарения любой
жидкости составляет величину порядка 88 Дж/(моль.
К).
Если при испарении разных жидкостей не
происходит ассоциации или диссоциации молекул,
то энтропия испарения будет приблизительно
одинакова. Для соединений, образующих водородные
связи (вода, спирты), энтропия испарения больше 88
Дж/(моль. К).
Правило Трутона позволяет определить
энтальпию испарения жидкости по известной
температуре кипения, а затем по уравнению
Клаузиуса-Клапейрона определить положение линии
моновариантного равновесия жидкость-пар на
фазовой диаграмме.
Задача 2. Оцените давление пара над
диэтиловым эфиром при 250С, зная его
температуру кипения ( 35.60С ).
Решение: Согласно правилу Трутона  Sисп = 88 Дж/(моль.К), с
другой стороны Sисп = 88 Дж/(моль.К), с
другой стороны  Sисп= Sисп= Hисп/Tкип; отсюда Hисп/Tкип; отсюда  Нисп=88.(35.6+273)=27.16
кДж/моль ( по справочнику Нисп=88.(35.6+273)=27.16
кДж/моль ( по справочнику  Нисп=26.6
кДж/моль ). Нисп=26.6
кДж/моль ).
Применим уравнение Клаузиуса-Клапейрона,
учитывая, что при кипении (Т=308.6К) давление паров
эфира р=1 атм. Тогда имеем ln p - ln 1 = 27.16.103/8.31(1/308.6-1/T),
или ln p = -3268/T + 10.59 ( и это является уравнением линии
моновариантного равновесия (жидкость)  (пар) на фазовой диаграмме эфира). Отсюда, при Т=298К
(250С) р=0.25 атм.
(пар) на фазовой диаграмме эфира). Отсюда, при Т=298К
(250С) р=0.25 атм.
Энтропия плавления не так постоянна для
разных веществ, как энтропия испарения. Это
связано с тем, что беспорядок ( мерой которого
является энтропия ) возрастает при переходе от
твердого к жидкому состоянию не столь сильно, как
при переходе в газообразное состояние.
|




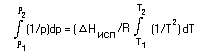 (14)
(14)