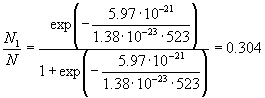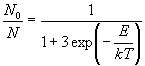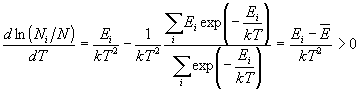|
Учебные материалы по физической химии
Задачи по физической химии.Часть 1.Химическая термодинамика
Глава 3. Статистическая термодинамика
10. Основные постулаты статистической
термодинамики
При описании систем, состоящих из большого
числа частиц, можно использовать два подхода:
микроскопический и макроскопический. В первом
подходе, основанном на классической или
квантовой механике, подробно характеризуется
микросостояние системы, например, координаты и
импульсы каждой частицы в каждый момент времени.
Микроскопическое описание требует решения
классических или квантовых уравнений движения
для огромного числа переменных. Так, каждое
микросостояние идеального газа в классической
механике описывается 6N переменными (N -
число частиц): 3N координат и 3N проекций
импульса.
Макроскопический подход, который использует
классическая термодинамика, характеризует
только макросостояния системы и использует для
этого небольшое число переменных, например, три:
температуру, объем и число частиц. Если система
находится в равновесном состоянии, то ее
макроскопические параметры постоянны, тогда как
микроскопические параметры изменяются со
временем. Это означает, что каждому
макросостоянию соответствует несколько (на
самом деле, бесконечно много) микросостояний.

Статистическая термодинамика устанавливает
связь между этими двумя подходами. Основная идея
заключается в следующем: если каждому
макросостоянию соответствует много
микросостояний, то каждое из них вносит в
макросостояние свой вклад. Тогда свойства
макросостояния можно рассчитать как среднее по
всем микросостояниям, т.е. суммируя их вклады с
учетом статистического веса.
Усреднение по микросостояниям проводят с
использованием понятия статистического
ансамбля. Ансамбль - это бесконечный набор
идентичных систем, находящихся во всех возможных
микросостояниях, соответствующих одному
макросостоянию. Каждая система ансамбля - это
одно микросостояние. Весь ансамбль описывается
некоторой функцией распределения по
координатам и импульсам  (p, q,
t), которая определяется следующим образом: (p, q,
t), которая определяется следующим образом:
 (p, q, t) dp dq - это
вероятность того, что система ансамбля находится
в элементе объема dp dq вблизи точки (p, q)
в момент времени t. (p, q, t) dp dq - это
вероятность того, что система ансамбля находится
в элементе объема dp dq вблизи точки (p, q)
в момент времени t.
Смысл функции распределения состоит в том,
что она определяет статистический вес каждого
микросостояния в макросостоянии.
Из определения следуют элементарные свойства
функции распределения:
1. Нормировка
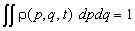 . (10.1) . (10.1)
2. Положительная определенность
 (p, q, t) і 0 (10.2) (p, q, t) і 0 (10.2)
Многие макроскопические свойства системы
можно определить как среднее значение функций
координат и импульсов f(p, q) по
ансамблю:
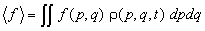 (10.3) (10.3)
Например, внутренняя энергия - это среднее
значение функции Гамильтона H(p,q):
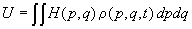 (10.4) (10.4)
Существование функции распределения
составляет суть основного постулата
классической статистической механики:
Макроскопическое состояние системы
полностью задается некоторой функцией
распределения, которая удовлетворяет условиям
(10.1) и (10.2).
Для равновесных систем и равновесных ансамблей
функция распределения не зависит явно от
времени:  = =  (p,q).
Явный вид функции распределения зависит от типа
ансамбля. Различают три основных типа ансамблей: (p,q).
Явный вид функции распределения зависит от типа
ансамбля. Различают три основных типа ансамблей:
1) Микроканонический ансамбль описывает
изолированные системы и характеризуется
переменными: E (энергия), V(объем), N(число
частиц). В изолированной системе все
микросостояния равновероятны (постулат равной
априорной вероятности):
 (10.5) (10.5)
2) Канонический ансамбль описывает системы,
находящиеся в тепловом равновесии с окружающей
средой. Тепловое равновесие характеризуется
температурой T. Поэтому функция
распределения также зависит от температуры:
 (10.6) (10.6)
(k = 1.38 10-23 Дж/К -
постоянная Больцмана). Значение константы в (10.6)
определяется условием нормировки (см. (11.2)). 10-23 Дж/К -
постоянная Больцмана). Значение константы в (10.6)
определяется условием нормировки (см. (11.2)).
Частным случаем канонического распределения
(10.6) является распределение Максвелла по
скоростям v, которое справедливо для газов:
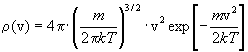 (10.7) (10.7)
(m - масса молекулы газа). Выражение  (v)dv описывает вероятность того,
что молекула имеет абсолютное значение скорости
в интервале от v до v + dv. Максимум функции (10.7)
дает наиболее вероятную скорость молекул, а
интеграл (v)dv описывает вероятность того,
что молекула имеет абсолютное значение скорости
в интервале от v до v + dv. Максимум функции (10.7)
дает наиболее вероятную скорость молекул, а
интеграл
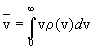 (10.8) (10.8)
- среднюю скорость молекул.
Если система имеет дискретные уровни энергии и
описывается квантовомеханически, то вместо
функции Гамильтона H(p,q) используют
оператор Гамильтона H, а вместо функции
распределения - оператор матрицы плотности  : :
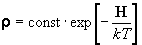 (10.9) (10.9)
Диагональные элементы матрицы плотности дают
вероятность того, что система находится в i-ом
энергетическом состоянии и имеет энергию Ei:
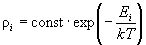 (10.10) (10.10)
Значение константы определяется условием
нормировки: S  i = 1: i = 1:
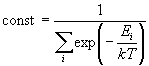 (10.11) (10.11)
Знаменатель этого выражения называют суммой по
состояниям (см. гл. 11). Он имеет ключевое значение
для статистической оценки термодинамических
свойств системы Из (10.10) и (10.11) можно найти число
частиц Ni, имеющих энергию Ei:
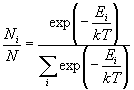 (10.12) (10.12)
(N - общее число частиц). Распределение
частиц (10.12) по уровням энергии называют распределением
Больцмана, а числитель этого распределения -
больцмановским фактором (множителем). Иногда это
распределение записывают в другом виде: если
существует несколько уровней с одинаковой
энергией Ei, то их объединяют в одну
группу путем суммирования больцмановских
множителей:
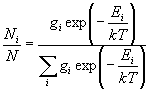 (10.13) (10.13)
(gi - число уровней с энергией Ei,
или статистический вес).
Многие макроскопические параметры
термодинамической системы можно вычислить с
помощью распределения Больцмана. Например,
средняя энергия определяется как среднее по
уровням энергии с учетом их статистических
весов:
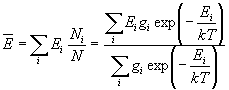 , (10.14) , (10.14)
3) Большой канонический ансамбль описывает
открытые системы, находящиеся в тепловом
равновесии и способные обмениваться веществом с
окружающей средой. Тепловое равновесие
характеризуется температурой T, а равновесие
по числу частиц - химическим потенциалом  . Поэтому функция распределения
зависит от температуры и химического потенциала.
Явное выражение для функции распределения
большого канонического ансамбля мы здесь
использовать не будем. . Поэтому функция распределения
зависит от температуры и химического потенциала.
Явное выражение для функции распределения
большого канонического ансамбля мы здесь
использовать не будем.
В статистической теории доказывается, что для
систем с большим числом частиц (~ 1023) все три
типа ансамблей эквивалентны друг другу.
Использование любого ансамбля приводит к одним и
тем же термодинамическим свойствам, поэтому
выбор того или иного ансамбля описания
термодинамической системы диктуется только
удобством математической обработки функций
распределения.
ПРИМЕРЫ
Пример 10-1. Молекула может находиться на
двух уровнях с энергиями 0 и 300 см-1. Какова
вероятность того, что молекула будет находиться
на верхнем уровне при 250 оС?
Решение. Надо применить распределение
Больцмана, причем для перевода
спектроскопической единицы энергии см-1 в
джоули используют множитель hc (h = 6.63 10-34 Дж. c, c = 3 10-34 Дж. c, c = 3 1010 см/с): 300 см-1 = 300 1010 см/с): 300 см-1 = 300  6.63 6.63 10-34 10-34  3 3 1010 = 5.97 1010 = 5.97 10-21 Дж. 10-21 Дж.
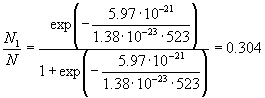
Ответ. 0.304.
Пример 10-2. Молекула может находиться на
уровне с энергией 0 или на одном из трех уровней с
энергией E. При какой температуре а) все
молекулы будут находиться на нижнем уровне, б)
число молекул на нижнем уровне будет равно числу
молекул на верхних уровнях, в) число молекул на
нижнем уровне будет в три раза меньше, чем число
молекул на верхних уровнях?
Решение. Воспользуемся распределением
Больцмана (10.13):
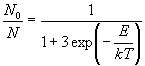
а) N0 / N = 1; exp(-E/kT) = 0; T = 0.
При понижении температуры молекулы
накапливаются на нижних уровнях.
б) N0 / N = 1/2; exp(-E/kT) = 1/3; T = E
/ [k ln(3)].
в) N0 / N = 1/4; exp(-E/kT) = 1; T =  . При высоких температурах молекулы
равномерно распределены по уровням энергии, т.к.
все больцмановские множители почти одинаковы и
равны 1. . При высоких температурах молекулы
равномерно распределены по уровням энергии, т.к.
все больцмановские множители почти одинаковы и
равны 1.
Ответ. а) T = 0; б) T = E / [k ln(3)]; в) T
=  . .
Пример 10-3. При нагревании любой
термодинамической системы заселенность одних
уровней увеличивается, а других уменьшается.
Используя закон распределения Больцмана,
определите, какова должна быть энергия уровня
для того, чтобы его заселенность увеличивалась с
ростом температуры.
Решение. Заселенность - доля молекул,
находящихся на определенном энергетическом
уровне. По условию, производная от этой величины
по температуре должна быть положительна:
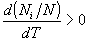
В данном случае оказывается удобнее считать
производную не самой заселенности, а ее
логарифма (если функция - возрастающая, то ее
логарифм тоже возрастает). Из распределения (10.12)
следует:
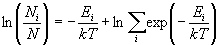
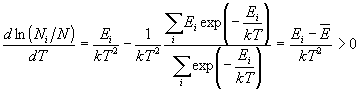
Во второй строчке мы использовали определение
средней энергии (10.14). Таким образом, заселенность
возрастает с ростом температуры для всех
уровней, превышающих среднюю энергию системы.
Ответ. 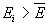 . .
ЗАДАЧИ
10-1. Молекула может находиться на двух
уровнях с энергиями 0 и 100 см-1. Какова
вероятность того, что молекула будет находиться
на низшем уровне при 25 оС?
10-2. Молекула может находиться на двух уровнях
с энергиями 0 и 600 см-1. При какой температуре
на верхнем уровне будет в два раза меньше
молекул, чем на нижнем?
10-3. Молекула может находиться на уровне с
энергией 0 или на одном из трех уровней с энергией
E. Найдите среднюю энергию молекул: а) при
очень низких температурах, б) при очень высоких
температурах.
10-4. При охлаждении любой термодинамической
системы заселенность одних уровней
увеличивается, а других уменьшается. Используя
закон распределения Больцмана, определите,
какова должна быть энергия уровня для того, чтобы
его заселенность увеличивалась с уменьшением
температуры.
10-5. Рассчитайте наиболее вероятную скорость
молекул углекислого газа при температуре 300 К.
10-6. Рассчитайте среднюю скорость атомов
гелия при нормальных условиях.
10-7. Рассчитайте наиболее вероятную скорость
молекул озона при температуре -30 оС.
10-8. При какой температуре средняя скорость
молекул кислорода равна 500 м/с?
10-9. При некоторых условиях средняя скорость
молекул кислорода равна 400 м/с. Чему равна средняя
скорость молекул водорода при этих же условиях?
10-10. Какова доля молекул массой m, имеющих
скорость выше средней при температуре T?
Зависит ли эта доля от массы молекул и
температуры?
10-11. Пользуясь распределением Максвелла,
рассчитайте среднюю кинетическую энергию
движения молекул массой m при температуре T.
Равна ли эта энергия кинетической энергии при
средней скорости?
|


 (10.5)
(10.5)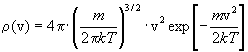 (10.7)
(10.7)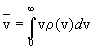 (10.8)
(10.8)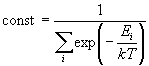 (10.11)
(10.11)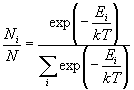 (10.12)
(10.12)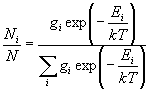 (10.13)
(10.13)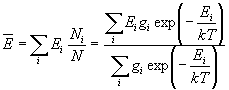 , (10.14)
, (10.14)