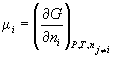|
Учебные материалы по физической химии
Задачи по физической химии.Часть 1.Химическая термодинамика
7. Растворы неэлектролитов
Состав растворов обычно выражают в весовых
процентах, в молях растворенного вещества на
литр раствора (молярность) или на килограмм
растворителя (моляльность), а также в мольных
долях.
Согласно закону Рауля, давление пара
растворителя P1 над раствором пропорционально
мольной доле растворителя X1 в растворе:
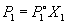
где 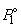 – давление пара
чистого растворителя при данной температуре. Для
бинарного раствора закон Рауля можно
представить в следующем виде: – давление пара
чистого растворителя при данной температуре. Для
бинарного раствора закон Рауля можно
представить в следующем виде:
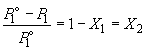 , ,
то есть относительное понижение давления пара
растворителя над раствором равно мольной доле X2
растворенного вещества.
Если оба компонента раствора летучи, то закон
Рауля выполняется для каждого из компонентов:
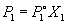
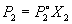 . .
Общее давление пара над раствором равно сумме парциальных
давлений P1 и P2:
P = P1 + P2 = 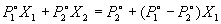 , ,
то есть давление пара линейно зависит от
состава раствора.
В идеальных растворах закон Рауля
выполняется для обоих компонентов во всем
интервале составов.
В реальных предельно разбавленных
растворах для растворителя выполняется закон
Рауля, а для растворенного вещества выполняется закон
Генри:
P2 = K2X2,
где K2 – константа Генри. В идеальных
растворах закон Генри совпадает с законом Рауля (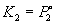 ). ).
Для описания свойств реальных растворов
вводится понятие активности. Активность ai
выражается в виде произведения мольной доли Xi
компонента на его коэффициент активности
 i: i:
ai =  iXi. iXi.
Коэффициенты активности растворителя можно
рассчитать на основании отклонений от закона
Рауля:
 i = i = 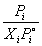 . .
При Xi  1 1  i i  1, то есть ai 1, то есть ai  Xi. Xi.
Коэффициенты активности растворенного
вещества можно рассчитать на основании
отклонений от закона Генри:
 i = i = 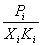 . .
При Xi  0 0  i i  1, то есть ai 1, то есть ai  Xi. Xi.
Вклад компонента в любое экстенсивное свойство
Z раствора определяется его парциальной
мольной величиной. Парциальная мольная
величина i-го компонента отражает изменение
свойства Z при изменении количества i-го
компонента на dni при постоянных P, T
и составе в расчете на 1 моль:
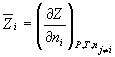
Общее значение свойства Z выражается суммой
вкладов всех компонентов:
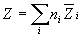
Парциальная мольная энергия Гиббса называется
химическим потенциалом  : :
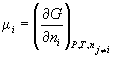
Парциальные мольные величины компонентов при
постоянных P и T связаны уравнением
Гиббса-Дюгема:
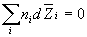
ПРИМЕРЫ
Пример 7-1. Рассчитать состав раствора
бензол – толуол, который при нормальном давлении
кипит при температуре 100o C, а также состав
образующегося пара. Раствор считать идеальным.
Давления пара чистых бензола и толуола при 100o
C равны 1350 Торр и 556 Торр соответственно.
Решение. Мольную долю бензола в растворе
находим по закону Рауля:
760 = 556 + (1350 – 556). X1, откуда X1
= 0.257.
Мольная доля толуола в растворе равна X2
= 1 – X1 = 0.743.
Мольная доля бензола в паре равна
Y1 = 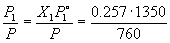 = 0.456 = 0.456
Соответственно, мольная доля толуола в паре
равна Y 2 = 1 – Y1 = 0.544.
Пример 7-2. Мольные объемы CCl4 и C6H6
равны 0.09719 и 0.08927 л. моль–1
соответственно, а их парциальные мольные объемы
в эквимолярном растворе равны 0.10010 и 0.10640 л.
моль–1. Рассчитать мольный объем
эквимолярного раствора и изменение объема при
смешении.
Решение. Объем раствора равен
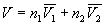 = 0.5. 0.10010 + 0.5.
0.10640 = 0.10325 (л. моль–1). = 0.5. 0.10010 + 0.5.
0.10640 = 0.10325 (л. моль–1).
Общий объем до смешения V0 = 0.5.
0.09719 + 0.5. 0.08927 = 0.09323 (л. моль–1).
 Vсмеш. = V
– V0 = 0.10325 – 0.09323 = 0.01002 (л. моль–1). Vсмеш. = V
– V0 = 0.10325 – 0.09323 = 0.01002 (л. моль–1).
ЗАДАЧИ
- Давления пара чистых CHCl3 и CCl4 при 25o
C равны 26.54 и 15.27 кПа. Полагая, что они образуют
идеальный раствор, рассчитать давление пара и
состав (в мольных долях) пара над раствором,
состоящим из 1 моль CHCl3 и 1 моль CCl4.
- Дибромэтилен и дибромпропилен при смешении
образуют почти идеальные растворы. При 80o C
давление пара дибромэтилена равно 22.9 кПа, а
дибромпропилена 16.9 кПа. Рассчитать состав пара,
находящегося в равновесии с раствором, мольная
доля дибромэтилена в котором равна 0.75.
Рассчитать состав раствора, находящегося в
равновесии с паром, мольная доля дибромэтилена в
котором равна 0.50.
- Этанол и метанол при смешении образуют почти
идеальные растворы. При 20o C давление пара
этанола равно 5.93 кПа, а метанола 11.83 кПа.
Рассчитать давление пара раствора, состоящего из
100 г этанола и 100 г метанола, а также состав (в
мольных долях) пара над этим раствором при 20o
C.
- Давления пара чистых бензола и толуола при 60o
C равны 51.3 и 18.5 кПа. При каком давлении закипит при
60o C раствор, состоящий из 1 моля бензола и 2
молей толуола? Каков будет состав пара?
- Давления пара чистых C6H5Cl и C6H5Br
при 140o C равны 1.237 бар и 0.658 бар. Рассчитать
состав раствора C6H5Cl – C6H5Br,
который при давлении 1 бар кипит при температуре
140o C, а также состав образующегося пара.
Каково будет давление пара над раствором,
полученным конденсацией образующегося пара?
- Константа Генри для CO2 в воде при 25o C
равна 1.25
 106
Торр. Рассчитать растворимость (в единицах
моляльности) CO2 в воде при 25o C, если
парциальное давление CO2 над водой равно 0.1
атм. 106
Торр. Рассчитать растворимость (в единицах
моляльности) CO2 в воде при 25o C, если
парциальное давление CO2 над водой равно 0.1
атм.
- Константы Генри для кислорода и азота в воде при
25o C равны 4.40
 109
Па и 8.68 109
Па и 8.68 109 Па
соответственно. Рассчитать состав (в %) воздуха,
растворенного в воде при 25o C, если воздух
над водой состоит из 80% N2 и 20% O2 по
объему, а его давление равно 1 бар. 109 Па
соответственно. Рассчитать состав (в %) воздуха,
растворенного в воде при 25o C, если воздух
над водой состоит из 80% N2 и 20% O2 по
объему, а его давление равно 1 бар.
- Константы Генри для кислорода и азота в воде при
0o C равны 2.54
 104
бар и 5.45 104
бар и 5.45 104 бар
соответственно. Рассчитать понижение
температуры замерзания воды, вызванное
растворением воздуха, состоящего из 80% N2 и
20% O2 по объему при давлении 1.0 бар.
Криоскопическая константа воды равна 1.86 К.
кг. моль–1. 104 бар
соответственно. Рассчитать понижение
температуры замерзания воды, вызванное
растворением воздуха, состоящего из 80% N2 и
20% O2 по объему при давлении 1.0 бар.
Криоскопическая константа воды равна 1.86 К.
кг. моль–1.
- При 25o C давление пара хлорметана над его
раствором в углеводороде при разных мольных
долях следующее:
| XCH3Cl (р-р) |
0.005 |
0.009 |
0.019 |
0.024 |
| PCH3Cl, Торр |
205 |
363 |
756 |
946 |
Показать, что в этом интервале мольных долей
раствор подчиняется закону Генри и рассчитать
константу Генри.
- При 57.2o C и давлении 1.00 атм мольная доля
ацетона в паре над раствором ацетон-метанол с
мольной долей ацетона в растворе XА = 0.400
равна YА = 0.516. Рассчитать активности и
коэффициенты активности обоих компонентов в
этом растворе на основе закона Рауля. Давления
пара чистых ацетона и метанола при этой
температуре равны 786 и 551 Торр соответственно.
- Для раствора этанол – хлороформ при 35o C
получены следующие данные:
| Xэтанола (р-р) |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
| Yэтанола (пар) |
0 |
0.1382 |
0.1864 |
0.2554 |
0.4246 |
1.0000 |
| Pобщее, кПа |
39.345 |
40.559 |
38.690 |
34.387 |
25.357 |
13.703 |
Рассчитать коэффициенты активности обоих
компонентов в растворе на основе закона Рауля.
- Для раствора CS2 – ацетон при 35.2o C
получены следующие данные:
| XCS2 (р-р) |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
| PCS2, кПа |
0 |
37.3 |
50.4 |
56.7 |
61.3 |
68.3 |
| Pацетона, кПа |
45.9 |
38.7 |
34.0 |
30.7 |
25.3 |
0 |
Рассчитать коэффициенты активности обоих
компонентов в растворе на основе закона Рауля.
- *Для раствора вода – н-пропанол при 25o C
получены следующие данные:
| Xн-пропанола (р-р) |
0 |
0.02 |
0.05 |
0.10 |
0.20 |
0.40 |
0.60 |
0.80 |
1.00 |
| Pводы, кПа |
3.17 |
3.13 |
3.09 |
3.03 |
2.91 |
2.89 |
2.65 |
1.79 |
0.00 |
| Pн-пропанола, кПа |
0.00 |
0.67 |
1.44 |
1.76 |
1.81 |
1.89 |
2.07 |
2.37 |
2.90 |
Рассчитать активности и коэффициенты
активности обоих компонентов в растворе с
мольной долей н-пропанола 0.20, 0.40, 0.60 и 0.80 на
основе законов Рауля и Генри, считая воду
растворителем.
- Парциальные мольные объемы воды и метанола в
растворе с мольной долей метанола 0.4 равны 17.35 и
39.01 см3. моль–1 соответственно.
Рассчитать объем раствора, содержащего 0.4 моль
метанола и 0.6 моль воды, а также объем до смешения.
Плотности воды и метанола равны 0.998 и 0.791 г.
см–3 соответственно.
- Парциальные мольные объемы воды и этанола в
растворе с мольной долей этанола 0.2 равны 17.9 и 55.0
см3. моль–1 соответственно.
Рассчитать объемы воды и этанола, необходимые
для приготовления 1 л такого раствора. Плотности
воды и этанола равны 0.998 и 0.789 г. см–3
соответственно.
- Парциальные мольные объемы ацетона и
хлороформа в растворе с мольной долей хлороформа
0.4693 равны 74.166 и 80.235 см3. моль–1
соответственно. Рассчитать объем такого
раствора, имеющего массу 1 кг.
- Плотность 50% (по массе) раствора этанола в воде
при 25o C равна 0.914 г. см–3.
Рассчитать парциальный мольный объем этанола в
этом растворе, если парциальный мольный объем
воды равен 17.4 см3. моль–1.
- Общий объем раствора этанола, содержащего 1.000 кг
воды, при 25o C описывается выражением
V(мл) = 1002.93 + 54.6664 m – 0.36394 m2
+ 0.028256 m3,
где m – моляльность раствора. Рассчитать
парциальные мольные объемы воды и этанола в
растворе, состоящем из 1.000 кг воды и 0.500 кг
этанола.
- Парциальный мольный объем K2SO4 в
водном растворе при 25o C описывается
выражением
V(см3. моль–1) = 32.28 +
18.216 m1/2,
где m – моляльность раствора. Используя
уравнение Гиббса-Дюгема, получите выражение для
парциального мольного объема воды в этом
растворе. Мольный объем чистой воды при 25o C
равен 18.079 см3. моль–1.
|

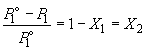 ,
,