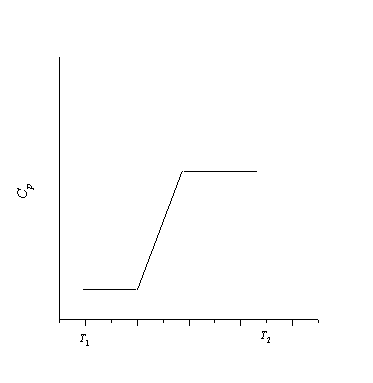|
Учебные материалы по физической химии
Задачи по физической химии.Часть 1.Химическая термодинамика
4. Второй закон термодинамики. Энтропия
Второй закон термодинамики устанавливает
критерии необратимости термодинамических
процессов. Известно много формулировок второго
закона, которые эквивалентны друг другу. Мы
приведем здесь только одну формулировку,
связанную с энтропией.
Существует функция состояния -
энтропия S, которая обладает следующим
свойством:  , (4.1) где
знак равенства относится к обратимым процессам,
а знак больше - к необратимым. , (4.1) где
знак равенства относится к обратимым процессам,
а знак больше - к необратимым.
Для изолированных систем второй закон
утверждает: dS і 0, (4.2) т.е. энтропия
изолированных систем в необратимых процессах
может только возрастать, а в состоянии
термодинамического равновесия она достигает
максимума (dS = 0,
d 2S < 0).
Неравенство (4.1) называют неравенством
Клаузиуса. Поскольку энтропия - функция
состояния, ее изменение в любом циклическом
процессе равно 0, поэтому для циклических
процессов неравенство Клаузиуса имеет вид:
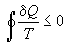 , (4.3) , (4.3)
где знак равенства ставится, если весь цикл
полностью обратим.
Энтропию можно определить с помощью двух
эквивалентных подходов - статистического и
термодинамического. Статистическое
определение основано на идее о том, что
необратимые процессы в термодинамике вызваны
переходом в более вероятное состояние, поэтому
энтропию можно связать с вероятностью:
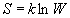 , (4.4) , (4.4)
где k = 1.38 10-23 Дж/К - постоянная
Больцмана (k = R / NA), W - так
называемая термодинамическая вероятность, т.е.
число микросостояний, которые соответствуют
данному макросостоянию системы (см. гл. 10).
Формулу (4.4) называют формулой Больцмана. 10-23 Дж/К - постоянная
Больцмана (k = R / NA), W - так
называемая термодинамическая вероятность, т.е.
число микросостояний, которые соответствуют
данному макросостоянию системы (см. гл. 10).
Формулу (4.4) называют формулой Больцмана.
С точки зрения строгой статистической
термодинамики энтропию вводят следующим
образом:
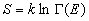 , (4.5) , (4.5)
где G (E) - фазовый объем, занятый
микроканоническим ансамблем с энергией E.
Термодинамическое определение энтропии
основано на рассмотрении обратимых процессов:
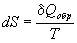 . (4.6) . (4.6)
Это определение позволяет представить
элементарную теплоту в такой же форме, как и
различные виды работы:
 Qобр = TdS, (4.7) Qобр = TdS, (4.7)
где температура играет роль обобщенной силы, а
энтропия - обобщенной (тепловой) координаты.
Расчет изменения энтропии для
различных процессов
Термодинамические расчеты изменения энтропии
основаны на определении (4.6) и на свойствах
частных производных энтропии по
термодинамическим параметрам:
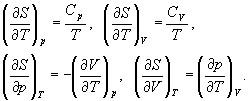 (4.8) (4.8)
Последние два тождества представляют собой соотношения
Максвелла (вывод см. в гл. 5).
1) Нагревание или охлаждение при постоянном
давлении.
Количество теплоты, необходимое для изменения
температуры системы, выражают с помощью
теплоемкости:  Qобр = Cp
dT. Qобр = Cp
dT.
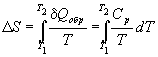 (4.9) (4.9)
Если теплоемкость не зависит от температуры в
интервале от T1 до T2, то
уравнение (4.8) можно проинтегрировать:
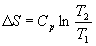 . (4.10) . (4.10)
Если изменение температуры происходит при
постоянном объеме, то в формулах (4.9) и (4.10) Cp
надо заменить на CV.
2) Изотермическое расширение или сжатие.
Для расчета энтропии в этом случае надо знать
уравнение состояния системы. Расчет основан на
использовании соотношения Максвелла:
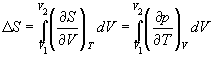 (4.11) (4.11)
В частности, для изотермического расширения
идеального газа (p = nRT / V)
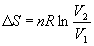 (4.12) (4.12)
Этот же результат можно получить, если
использовать выражение для теплоты
изотермического обратимого расширения
идеального газа: Qобр = nRT ln(V2/V1).
3) Фазовые переходы.
При обратимом фазовом переходе температура
остается постоянной, а теплота фазового перехода
при постоянном давлении равна  Hфп,
поэтому изменение энтропии равно: Hфп,
поэтому изменение энтропии равно:
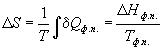 (4.13) (4.13)
При плавлении и кипении теплота поглощается,
поэтому энтропия в этих процессах возрастает: Sтв
< Sж < Sг. При этом энтропия
окружающей среды уменьшается на величину  Sф.п., поэтому изменение
энтропии Вселенной равно 0, как и полагается для
обратимого процесса в изолированной системе. Sф.п., поэтому изменение
энтропии Вселенной равно 0, как и полагается для
обратимого процесса в изолированной системе.
4) Смешение идеальных газов при постоянных
температуре и давлении.
Если n1 молей одного газа, занимающего
объем V1, смешиваются с n2
молями другого газа, занимающего объем V2,
то общий объем будет равен V1 + V2,
причем газы расширяются независимо друг от друга
и общее изменение энтропии равно сумме изменений
энтропии каждого газа:
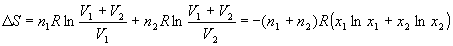 , (4.14) , (4.14)
где xi - мольная доля i-го газа в
полученной газовой смеси. Изменение энтропии (4.14)
всегда положительно, т.к. все ln xi < 0,
поэтому идеальные газы всегда смешиваются
необратимо.
Если при тех же условиях смешиваются две порции
одного и того же газа, то уравнение (4.14) уже
неприменимо. Никаких изменений в системе при
смешивании не происходит, и  S
= 0. Тем не менее, формула (4.14) не содержит никаких
индивидуальных параметров газов, поэтому,
казалось бы, должна быть применима и к смешению
одинаковых газов. Это противоречие называют парадоксом
Гиббса. S
= 0. Тем не менее, формула (4.14) не содержит никаких
индивидуальных параметров газов, поэтому,
казалось бы, должна быть применима и к смешению
одинаковых газов. Это противоречие называют парадоксом
Гиббса.
Абсолютная энтропия
В отличие от многих других термодинамических
функций, энтропия имеет точку отсчета, которая
задается постулатом Планка (третьим законом
термодинамики):
При абсолютном нуле T = 0 К все
идеальные кристаллы
имеют одинаковую энтропию, равную нулю.
При стремлении температуры к абсолютному нулю
не только энтропия стремится к 0, но и ее
производные по всем термодинамическим
параметрам:
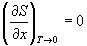 (x = p, V).
(4.15) (x = p, V).
(4.15)
Это означает, что вблизи абсолютного нуля все
термодинамические процессы протекают без
изменения энтропии. Это утверждение называют тепловой
теоремой Нернста.
Постулат Планка позволяет ввести понятие абсолютной
энтропии вещества, т.е. энтропии, отсчитанной
от нулевого значения при T = 0. Для расчета
абсолютной энтропии веществ в стандартном
состоянии надо знать зависимости теплоемкости Cp
от температуры для каждой из фаз, а также
температуры и энтальпии фазовых переходов. Так,
например, абсолютная энтропия газообразного
вещества в стандартном состоянии при
температуре T складывается из следующих
составляющих:
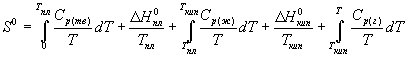 (4.16) (4.16)
В термодинамических таблицах обычно приводят
значения абсолютной энтропии в стандартном
состоянии при температуре 298 К.
Значения абсолютной энтропии веществ
используют для расчета изменения энтропии в
химических реакциях:
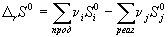 . (4.17) . (4.17)
ПРИМЕРЫ
Пример 4-1. Определите зависимость энтропии
от объема для термодинамической системы, которая
описывается уравнением состояния (для одного
моля)
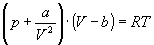
Решение.
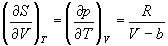
Интегрируя это равенство, находим зависимость
энтропии от объема:
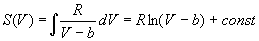 , ,
где const зависит от температуры.
Пример 4-2. Рассчитайте изменение энтропии
при нагревании 0.7 моль моноклинной серы от 25 до 200 оС
при давлении 1 атм. Мольная теплоемкость серы
равна:
Cp(Sтв) = 23.64 Дж/(моль.
К),
Cp(Sж) = 35.73 + 1.17. 10-3. T
Дж/(моль. К).
Температура плавления моноклинной серы 119 оС,
удельная теплота плавления 45.2 Дж/г.
Решение. Общее изменение энтропии
складывается из трех составляющих: 1) нагревание
твердой серы от 25 до 119 оС, 2) плавление, 3)
нагревание жидкой серы от 119 до 200 оС.
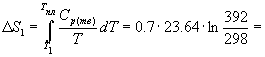 4.54 Дж/К. 4.54 Дж/К.
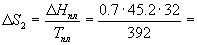 2.58 Дж/К. 2.58 Дж/К.
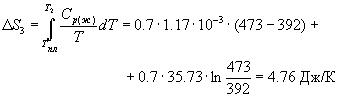
 S = S =  S1
+ S1
+  S2 + S2 +  S3 = 11.88 Дж/К.
S3 = 11.88 Дж/К.
Ответ. 11.88 Дж/К.
Пример 4-3. Найдите изменение энтропии газа и
окружающей среды, если n молей идеального
газа расширяются изотермически от объема V1
до объема V2: а) обратимо; б) против
внешнего давления p.
Решение. а) Изменение энтропии газа при
обратимом изотермическом расширении можно найти
с помощью термодинамического определения
энтропии с расчетом теплоты расширения по
первому закону:
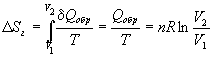 . .
Так как расширение обратимое, то общее
изменение энтропии Вселенной равно 0, поэтому
изменение энтропии окружающей среды равно
изменению энтропии газа с обратным знаком:
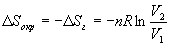 . .
б) Энтропия - функция состояния, поэтому
изменение энтропии системы не зависит от того,
как совершался процесс - обратимо или необратимо.
Изменение энтропии газа при необратимом
расширении против внешнего давления будет таким
же, как и при обратимом расширении. Другое дело -
энтропия окружающей среды, которую можно найти,
рассчитав с помощью первого закона теплоту,
переданную системе:
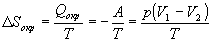 . .
В этом выводе мы использовали тот факт, что  U = 0 (температура постоянна).
Работа, совершаемая системой против постоянного
внешнего давления равна: A = p(V2-V1),
а теплота, принятая окружающей средой, равна
работе, совершенной системой, с обратным знаком. U = 0 (температура постоянна).
Работа, совершаемая системой против постоянного
внешнего давления равна: A = p(V2-V1),
а теплота, принятая окружающей средой, равна
работе, совершенной системой, с обратным знаком.
Общее изменение энтропии газа и окружающей
среды больше 0:
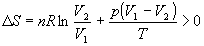 , ,
как и полагается для необратимого процесса.
Пример 4-4. Рассчитайте изменение энтропии
1000 г воды в результате ее замерзания при -5 ОС.
Теплота плавления льда при 0 оС равна 6008
Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3
Дж/(моль. К), соответственно. Объясните,
почему энтропия при замерзании уменьшается, хотя
процесс - самопроизвольный.
Решение. Необратимый процесс замерзания
воды при температуре -5 ОС можно
представить в виде последовательности обратимых
процессов: 1) нагревание воды от
-5 ОС до температуры замерзания (0 ОС);
2) замерзание воды при 0 ОС; 3) охлаждение
льда от 0 до -5 ОС:
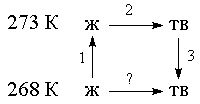
Изменение энтропии в первом и третьем
процессах (при изменении температуры)
рассчитывается по формуле (4.9):
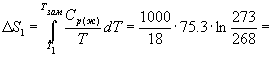 77.3 Дж/К. 77.3 Дж/К.
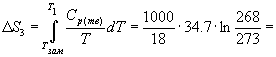 -35.6 Дж/К. -35.6 Дж/К.
Изменение энтропии во втором процессе
рассчитывается как для обычного фазового
перехода (4.13). Необходимо только иметь в виду, что
теплота при замерзании выделяется:
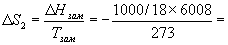 -1223 Дж/К. -1223 Дж/К.
Т.к. энтропия - функция состояния, общее
изменение энтропии равно сумме по этим трем
процессам:
 S = S =  S1
+ S1
+  S2 + S2 +  S3 = -1181 Дж/К.
S3 = -1181 Дж/К.
Энтропия при замерзании убывает, хотя процесс
самопроизвольный. Это связано с тем, что в
окружающую среду выделяется теплота и энтропия
окружающей среды увеличивается, причем это
увеличение больше, чем 1181 Дж/К, поэтому энтропия
Вселенной при замерзании воды возрастает, как и
полагается в необратимом процессе.
Ответ. -1181 Дж/К.
ЗАДАЧИ
4-1. Приведите пример термодинамического
процесса, который может быть проведен как
обратимо, так и необратимо. Рассчитайте
изменение энтропии системы и окружающей среды в
обоих случаях.
4-2. Проверьте неравенство Клаузиуса для
циклического процесса, представленного в задаче
2.14.
4-3. Рассчитайте мольную энтропию неона при 500
К, если при 298 К и том же объеме энтропия неона
равна 146.2 Дж/(моль. К).
4-4. Рассчитайте изменение энтропии при
нагревании 11.2 л азота от 0 до 50 оС и
одновременном уменьшении давления от 1 атм до 0.01
атм.
4-5. Один моль гелия при 100 оС и 1 атм
смешивают с 0.5 моль неона при 0 оС и 1 атм.
Определите изменение энтропии, если конечное
давление равно 1 атм.
4-6. Рассчитайте изменение энтропии при
образовании 1 м3 воздуха из азота и
кислорода (20 об.%) при температуре 25 оС и
давлении 1 атм.
4-7. Три моля идеального одноатомного газа (CV
= 3.0 кал/(моль. К)), находящегося при T1
= 350 K и P1 = 5.0 атм, обратимо и
адиабатически расширяются до давления P2
= 1.0 атм. Рассчитайте конечные температуру и
объем, а также совершенную работу и изменение
внутренней энергии, энтальпии и энтропии в этом
процессе.
4-8. Рассчитайте изменение энтропии при
нагревании 0.4 моль хлорида натрия от 20 до 850 оС.
Мольная теплоемкость хлорида натрия равна:
Cp(NaClтв) = 45.94 + 16.32. 10-3.
T Дж/(моль. К),
Cp(NaClж) = 66.53 Дж/(моль. К).
Температура плавления хлорида натрия 800 оС,
теплота плавления 31.0 кДж/моль.
4-9. Рассчитайте изменение энтропии при
смешении 5 кг воды при 80 оС с 10 кг воды при 20 оС.
Удельную теплоемкость воды принять равной: Cp(H2O)
= 4.184 Дж/(г. К).
4-10. Рассчитайте изменение энтропии при
добавлении 200 г льда, находящегося при
температуре 0 оС, к 200 г воды (90 оС) в
изолированном сосуде. Теплота плавления льда
равна 6.0 кДж/моль.
4-11. Для некоторого твердого тела найдена
зависимость коэффициента расширения от давления
в интервале давлений от p1 до p2:
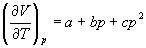 . .
Насколько уменьшится энтропия этого тела при
сжатии от p1 до p2?
4-12. Найдите изменение энтропии газа и
окружающей среды, если n молей идеального
газа расширяются изотермически от давления p1
до давления p2: а) обратимо; б) против
внешнего давления p < p2.
4-13. Запишите выражение для расчета
абсолютной энтропии одного моля воды при
температуре 300 0С и давлении 2 атм.
4-14. Нарисуйте график зависимости стандартной
энтропии воды от температуры в интервале от 0 до
400 К.
4-15. Запишите энтропию одного моля идеального
газа как функцию температуры и давления
(теплоемкость считать постоянной).
4-16. Определите зависимость энтропии от
объема для термодинамической системы, которая
описывается уравнением состояния (для одного
моля):
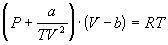
4-17. Определите зависимость энтропии от
объема для термодинамической системы, которая
описывается уравнением состояния (для одного
моля):
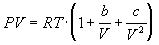
4-18. Один моль газа описывается уравнением
состояния
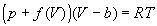 , ,
где f(V) - некоторая функция, которая не
зависит от температуры. Рассчитайте изменение
энтропии газа при его необратимом
изотермическом расширении от объема V1
до объема V2.
4-19. Рассчитайте изменение энтропии 1000 г
метанола в результате его замерзания при -105 ОС.
Теплота плавления твердого метанола при -98 оС
(т.пл.) равна 3160 Дж/моль. Теплоемкости твердого и
жидкого метанола равны 55.6 и 81.6 Дж/(моль. К),
соответственно. Объясните, почему энтропия при
замерзании уменьшается, хотя процесс -
самопроизвольный.
4-20. Теплоемкость некоторого вещества в
интервале температур от T1 до T2
изменяется следующим образом:
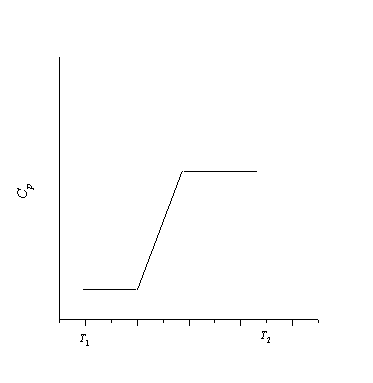
Постройте график зависимости энтропии
вещества от температуры в этом интервале
температур.
4-21. Пользуясь справочными данными, приведите
пример самопроизвольной химической реакции, для
которой стандартное изменение энтропии меньше 0.
4-22. Пользуясь справочными данными,
рассчитайте стандартное изменение энтропии в
реакции H2(г) + ЅO2(г) = H2O(г) а)
при 25 оС; б) при 300 оС.
|

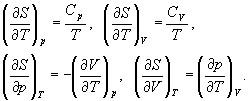 (4.8)
(4.8)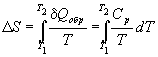 (4.9)
(4.9)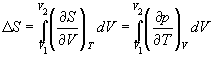 (4.11)
(4.11)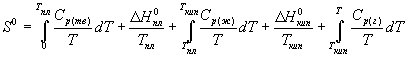 (4.16)
(4.16)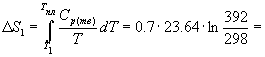 4.54 Дж/К.
4.54 Дж/К.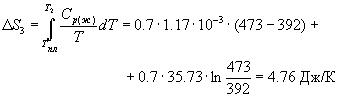
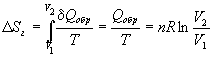 .
.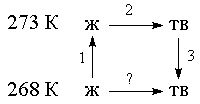
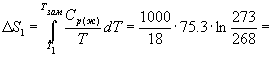 77.3 Дж/К.
77.3 Дж/К.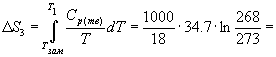 -35.6 Дж/К.
-35.6 Дж/К.