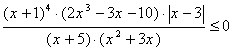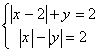Программа изучения математики в X и XI классах
Канд.физ.-мат.наук
В.Ю.Беляев, канд.технических наук Н.А.Романова, Ю.Г.Соколов
Программа изучения алгебры и начал анализа и
геометрии в химических классах школы № 171 составлена с учётом многолетнего
опыта проведения занятий по математике, накопленного в школе с 1974 года, когда
в школе начали работать химические классы, и с учётом требований, предъявляемых
химическим факультетом МГУ к математической подготовке учащихся.
Программа включает в себя как разделы повторения и
обобщения знаний, полученных учащимися в основной школе, так и изучения основ
современной алгебры, математического анализа и геометрии, направленного на
создание у учащихся устойчивого интереса к предмету, усвоения ими важнейших
математических понятий и их применения при решении различного рода прикладных
задач (химических, биологических, физических и т.д.).
Учащийся после завершения изучения алгебры и начал математического анализа
в 10 классе должен:
1.По теме "Модуль":
1.1. Давать определение модуля числа и его геометрическую
интерпретацию.
1.2. Уметь решать уравнения, неравенства и системы уравнений
и неравенств, содержащие знак модуля.
1.3. Уметь строить графики функций, содержащих модуль типа:
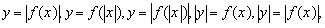 и т.п. и т.п.
2.По теме "Функции и их свойства":
2.1. Давать определение функции,
знать её способы задания.
2.2. Давать определения и уметь
находить области определения и области
значений функции.
2.3. Давать определение чётной и
нечётной функции, применять алгоритм определения функции на чётность и
нечётность.
2.4. Давать определение
возрастающей и убывающей функции, уметь определять промежутки монотонности
функций с помощью определения и используя график.
2.5. Давать определение
внутренних и граничных точек множества, приводить соответствующие примеры.
2.6. Давать определения точек
экстремума и экстремумов функции, уметь находить их для изученных функций.
2.7. Иметь понятие о характерных
точках, горизонтальных и вертикальных асимптотах.
2.8. Проводить исследование
изученных функций по схеме исследования функции и по графику.
3. По темам "Решение алгебраических уравнений, неравенств и их систем",
"Построение графиков функций":
3.1. Владеть методами построения
графиков функций (без использования производной).
3.2. Изображать на координатной
плоскости множество точек, удовлетворяющих заданным условиям.
3.3. Владеть методом равносильных
преобразований при решении алгебраических уравнений и неравенств.
3.4. Уметь решать
дробно-рациональные неравенства методом интервалов.
3.5. Применять теорему Безу и
следствия из неё при нахождении корней многочлена.
3.6. Знать и применять схему Горнера.
3.7. Уметь делить многочлен на
многочлен "уголком".
3.8. Уметь объяснить понятие
решения системы уравнений, совместной и несовместной системы уравнений.
3.9. Уметь решать системы
уравнений методами подстановки и сложения.
3.10. Давать определения и уметь
решать симметрические и однородные системы
уравнений.
3.11. Уметь решать системы
методом расщепления на более простые системы.
3.12. Уметь применять при решении
систем уравнений метод равносильных преобразований.
4. По теме "Степень и её
свойства":
4.1. Давать определение корня n-ой степени, формулировать и
доказывать его основные свойства.
4.2. Уметь проводить
преобразование выражений, содержащих знак корня.
4.3. Давать определение степени с
рациональным показателем, формулировать и доказывать её основные свойства.
4.4. Давать определение степени с
иррациональным показателем.
4.5. Уметь проводить
преобразования выражений, содержащих степени с рациональными и иррациональными
показателями.
4.6. Давать определение степенной
функции, строить график функции при различных основаниях, проводить
исследование данной функции.
4.7. Уметь решать иррациональные
уравнения типа: 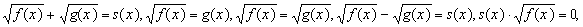 и уравнения смешанного типа. и уравнения смешанного типа.
4.8. Уметь решать иррациональные
неравенства типа: 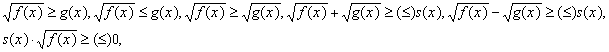 и неравенства смешанного типа. и неравенства смешанного типа.
5. По теме "Показательная функция":
5.1. Уметь давать определение
показательной функции, знать её основные свойства, уметь строить график
функции.
5.2. Уметь решать
показательные уравнения различного
типа, в том числе и с основаниями, зависящими от переменной.
5.3. Уметь решать показательные
неравенства различного типа, в том числе и с основаниями, зависящими от
переменной.
5.4. Уметь решать системы
показательных уравнений.
6. По теме "Логарифмическая функция":
6.1. Давать определение логарифма,
применять его при вычислении логарифма.
6.2. Формулировать и доказывать
свойства логарифмов, уметь применять свойства при преобразовании
логарифмических выражений, уметь переходить от одного основания логарифма к
другому.
6.3. Давать определение логарифмической функции, формулировать и доказывать её
свойства, уметь строить график функции.
6.4. Уметь решать логарифмические
уравнения различного типа, в том числе и содержащие переменную в основании.
6.5. Уметь решать логарифмические
неравенства различного типа, в том числе и содержащие переменную в основании.
6.6. Уметь решать системы
логарифмических уравнений и неравенств.
7. По теме
"Тригонометрические функции":
7.1. Давать определение синуса,
косинуса, тангенса и котангенса любого угла. Знать, уметь выводить и применять
основные тригонометрические формулы.
7.2. Знать значения
тригонометрических функций для углов 00, 300, 450,
600, 900, 1800, 2700, 3600.
7.3. Знать и уметь применять
формулы приведения.
7.4. Знать и уметь выводить
формулы сложения, двойного угла, формулы суммы и разности тригонометрических
функций. Уметь применять данные формулы при
преобразовании тригонометрических выражений.
7.5. Давать определение
тригонометрических функций, строить графики функций, содержащих "сжатие",
"растяжение", "сдвиг", "модуль", уметь проводить их исследование.
7.6. Давать определение и
находить значения арксинуса, арккосинуса, арктангенса и арккотангенса числа,
давать определения и знать свойства обратных
тригонометрических функций.
7.7. Уметь решать простейшие
тригонометрические уравнения, уравнения приводимые к алгебраическим, однородные
уравнения, уравнения, решаемые разложением на множители, с помощью формул
понижения степени, с помощью формул сложения и с помощью введения вспомогательного
угла.
7.8. Уметь решать системы
тригонометрических уравнений.
7.9. Уметь решать
тригонометрические неравенства.
Учащийся после
завершения изучения алгебры и начал
математического анализа в 11 лицейском химическом классе должен:
1. По теме "Производная. Вычисление производной":
1.1. Давать определение
окрестности точки, иллюстрировать определение на конкретных примерах.
1.2. Понимать, что такое
приращение функции и приращение аргумента, уметь находить приращение конкретных
функций.
1.3. Понимать, что такое
дифференциал функции, уметь находить его, используя приращение функции.
1.4. Давать определение предела
функции, его геометрическую иллюстрацию, иметь представление о нахождении
предела функции с помощью определения.
1.5. Давать различные определения
функции, непрерывной в точке (на языке
последовательности, на языке окрестности, если 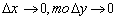 ). Приводить примеры. ). Приводить примеры.
1.6. Понимать, что такое
предельный переход, знать основные правила предельного перехода под знаком
непрерывной функции.
1.7. Уметь вычислять пределы и
раскрывать неопределённости вида 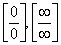 в простейших случаях. в простейших случаях.
1.8. Знать и уметь применять
первый замечательный предел.
1.9. Знать задачи, приводящие к
понятию производной.
1.10. Знать определение
производной, уметь вычислять производную с использованием её определения.
1.11. Знать и уметь объяснить
механический и геометрический смысл производной.
1.12. Знать, уметь обосновывать и
применять правила вычисления производных.
1.13. Знать, уметь выводить и
применять формулы для производных степенной функции, тригонометрических
функций, формулу для производной сложной функции.
1.14. Знать смысл числа е. Знать, уметь выводить и применять
формулы для производных показательной и логарифмической функций.
1.15. Знать механический смысл
второй производной, уметь находить производные высших порядков.
2. По теме "Применение непрерывности и производной":
2.1. Знать свойства функций,
непрерывных на интервале, уметь применять указанные свойства при решении
неравенств и численном решении уравнений.
2.2. Владеть алгоритмом решения
неравенств методом интервалов.
2.3. Владеть методом половинного
деления решения уравнений.
2.4. Давать определение
касательной к графику функции. Уметь выводить уравнение касательной, и решать
задачи на составление и использование
уравнения касательной в случаях: точка лежит на графике данной функции,
точка не лежит на графике, касательная параллельна данной прямой, определять в
каком случае прямая является касательной к графику данной функции.
2.5. Знать формулу Лагранжа и её
геометрический смысл.
2.6. Уметь находить дифференциал
функции с помощью производной, знать применения производной и дифференциала в
физике и технике.
3. По теме "Применение производной к исследованию функций":
3.1. Уметь формулировать,
доказывать и применять достаточный признак возрастания и убывания функции.
3.2. Уметь формулировать теорему
Дарбу и применять её при исследовании функций.
3.3. Давать определение
критических точек функции. Формулировать и применять теорему Ферма (необходимое
условие экстремума функции).
3.4. Знать, уметь обосновывать и
применять достаточные условия экстремума функции.
3.5. Знать формулировку теоремы
Ролля, уметь давать ей геометрическую иллюстрацию.
3.6. Давать определение асимптот
графика функции. Знать формулы для нахождения асимптот и уметь их применять при
нахождении вертикальных, горизонтальных и наклонных асимптот.
3.7. Знать и уметь применять при
исследовании функций условие выпуклости функций, уметь находить точки перегиба
функции.
3.8. Уметь проводить исследование
функций с помощью производной и на основании этого исследования строить графики
функций.
3.9. Знать формулировку теоремы
Вейерштрасса. Владеть алгоритмом нахождения наибольшего и наименьшего значений
функции на отрезке.
3.10. Уметь строить
математические модели текстовых задач, требующих владение алгоритмом нахождения
наибольшего и наименьшего значений функции на промежутке и проводить их
исследование.
4. По теме "Первообразная":
4.1. Давать определение
первообразной. Знать формулировку и уметь доказать основное свойство
первообразной и правила нахождения первообразных.
4.2. Знать определение
неопределённого интеграла, знать основные формулы для вычисления
неопределённого интеграла, уметь применять указанные формулы при нахождении первообразных
и вычислении неопределённого интеграла.
5. По теме "Определённый интеграл":
5.1. Давать определение
криволинейной трапеции. Приводить примеры криволинейных трапеций и уметь
определять: является ли данная фигура криволинейной трапецией.
5.2. Знать и уметь выводить
формулу для вычисления площади криволинейной трапеции. Уметь применять данную
формулу при решении практических задач.
5.3. Знать и понимать определение
определённого интеграла.
5.4. Знать и уметь выводить
формулу Ньютона-Лейбница.
5.5. Уметь вычислять определённые
интегралы и площади фигур с использованием формулы Ньютона-Лейбница.
5.6. Иметь представление о методе
прямоугольников и методе трапеций для вычисления площади криволинейной
трапеции.
5.7. Знать и уметь обосновывать
формулу для вычисления объёмов тел. Уметь вычислять объёмы тел с использованием
данной формулы в простейших случаях.
5.8. Уметь привести примеры
применения интеграла в физике.
5.9. Знать определение
дифференциального уравнения. Решать простейшие дифференциальные уравнения.
5.10. Уметь записывать и находить
решение дифференциального уравнения показательного роста и показательного
убывания (в том числе уравнение радиоактивного распада), уравнения гармонических
колебаний.
6. По теме "Решение задач с параметрами":
6.1. Понимать, что представляет собой
задача с параметрами.
6.2. Решать линейные уравнения и
неравенства, содержащие параметр.
6.3. Решать квадратные уравнения
и неравенства, содержащие параметр.
6.4. Решать более сложные
уравнения и неравенства, содержащие параметр.
6.5. Владеть графическим методом
решения задач с параметрами.
6.6. Уметь применять производную
при решении задач с параметрами.
6.7. Владеть методами поиска
необходимых условий.
6.8. Решать системы уравнений и
неравенств, содержащих параметр.
7. По теме "Основы комбинаторики и теории вероятностей":
7.1. Знать правило произведения и
уметь применять его при решении задач.
7.2. Понимать, что такое
сочетания и размещения. Знать формулы для их вычисления и уметь применять их
при решении задач.
7.3. Знать, что такое
перестановки и уметь их вычислять.
7.4. Давать классическое
определение вероятности. Уметь решать задачи на определение вероятности.
7.5. Понимать, что такое условная
вероятность. Решать задачи на вычисление условной вероятности.
7.6. Решать задачи на вероятность
суммы и произведения событий.
Примерное распределение учебных часов по алгебре и
началам анализа:
10-ый класс (всего 34
.5 = 170 уроков)
|
№ уроков
|
Тема
|
|
1-3
|
Повторение
(решение уравнений и неравенств, построение графиков элементарных функций)
|
|
Тема 1
|
Решение
алгебраических уравнений и неравенств. Построение графиков функций
|
|
4-7
|
Методы построения графиков функций.
|
|
8
|
Проверочная работа
|
|
9-12
|
Решение уравнений, содержащих знак модуля.
|
|
13-16
|
Решение неравенств, содержащих знак модуля.
|
|
17-19
|
Построение графиков функций, содержащих модуль.
|
|
20-21
|
Решение систем уравнений, содержащих модуль.
|
|
22
|
Проверочная работа
|
|
23-25
|
Решение дробно-рациональных неравенств.
|
|
26
|
Схема Горнера.
|
|
27-28
|
Теорема Безу и её следствия. Решение уравнений.
|
|
29
|
Подготовка к контрольной работе.
|
|
30-31
|
Контрольная работа №1
|
|
Тема 2
|
Функции
и их свойства
|
|
32
|
Область определения и область значений функции.
|
|
33
|
Чётные и нечётные функции.
|
|
34
|
Возрастание и убывание функций.
|
|
35
|
Точки экстремума и экстремумы функций.
|
|
36-37
|
Схема исследования функций.
|
|
38
|
Подготовка к контрольной работе.
|
|
39
|
Контрольная работа №2.
|
|
Тема 3
|
Степень
|
|
40-42
|
Корень n-ой степени и его свойства.
|
|
43-44
|
Степень с рациональным показателем.
|
|
45
|
Степень с иррациональным показателем.
|
|
46-48
|
Преобразование выражений.
|
|
49-50
|
Степенная функция, её свойства и график.
|
|
51
|
Проверочная работа.
|
|
52-56
|
Решение иррациональных уравнений.
|
|
57-61
|
Решение иррациональных неравенств.
|
|
62
|
Подготовка к контрольной работе.
|
|
63-64
|
Контрольная работа №3.
|
|
65
|
Анализ контрольной работы.
|
|
66-70
|
Методы решения систем уравнений.
|
|
71
|
Проверочная работа.
|
|
Тема 4.
|
Показательная
функция
|
|
72-73
|
Показательная функция, её свойства и график
|
|
74-77
|
Решение показательных уравнений
|
|
78-79
|
Решение систем уравнений
|
|
80-83
|
Решение показательных неравенств
|
|
84
|
Подготовка к контрольной работе
|
|
85-86
|
Контрольная работа №4
|
|
87
|
Анализ контрольной работы.
|
|
Тема 5.
|
Логарифмическая
функция
|
|
88-89
|
Логарифмы и их свойства.
|
|
90-93
|
Преобразование логарифмических выражений.
|
|
94-95
|
Логарифмическая функция и её свойства.
|
|
96-100
|
Решение логарифмических уравнений.
|
|
101
|
Проверочная работа.
|
|
102-106
|
Решение логарифмических неравенств.
|
|
107
|
Подготовка к контрольной работе.
|
|
108-109
|
Контрольная работа №5.
|
|
110
|
Анализ контрольной работы.
|
|
Тема 6
|
Тригонометрические
функции.
|
|
111
|
Синус, косинус, тангенс и котангенс.
|
|
112-114
|
Основные тригонометрические формулы. Формулы приведения.
|
|
115-116
|
Формулы сложения и двойного угла. Формулы суммы и
разности тригонометрических функций.
|
|
117-119
|
Преобразование тригонометрических выражений.
|
|
120
|
Проверочная работа.
|
|
121-123
|
Тригонометрические функции и их свойства.
|
|
124-127
|
Построение графиков тригонометрических функций.
Исследование функций.
|
|
128
|
Проверочная работа.
|
|
129-130
|
Обратные тригонометрические функции.
|
|
131-132
|
Простейшие тригонометрические уравнения.
|
|
133-134
|
Уравнения, приводимые к алгебраическим.
|
|
135-136
|
Однородные тригонометрические уравнения.
|
|
137-138
|
Уравнения, решаемые разложением на множители.
|
|
139-141
|
Решение тригонометрических уравнений (с помощью формул
понижения степени, сложения и введения вспомогательного угла).
|
|
142-143
|
Решение систем тригонометрических уравнений.
|
|
144-145
|
Контрольная работа №6.
|
|
146-149
|
Простейшие тригонометрические неравенства.
|
|
150-155
|
Повторение.
|
|
156-158
|
Итоговая контрольная работа.
|
|
159
|
Анализ контрольной
работы.
|
|
160-170
|
Решение конкурсных задач
|
11-ый класс (всего 34
. 4,5 = 153 урока)
|
№ уроков
|
Тема
|
|
1-6
|
Повторение
(Решение уравнений, неравенств, и их систем)
|
|
7
|
Проверочная работа.
|
|
Тема 1.
|
Производная
|
|
8-9
|
Приращение функции.
|
|
10-12
|
Предел и непрерывность функции. Предельный переход под
знаком непрерывной функции. Простейшие случаи вычисления пределов. Первый
замечательный предел.
|
|
13-14
|
Понятие производной, её геометрический и механический
смысл. Вычисление производной с использованием её определения.
|
|
15-16
|
Правила вычисления производных.
|
|
17
|
Производная степенной функции.
|
|
18-19
|
Производная сложной функции.
|
|
20-21
|
Производные тригонометрических функций.
|
|
22-23
|
Производная показательной функции. Число е.
|
|
24
|
Производная логарифмической функции.
|
|
25-27
|
Вычисление производных.
|
|
28
|
Вторая производная функции и производные высших порядков.
Дифференциал функции.
|
|
29
|
Проверочная работа.
|
|
Тема 2
|
Применение
непрерывности и производной
|
|
30
|
Свойства функций непрерывных на интервале. Метод
интервалов.
|
|
31-35
|
Решение неравенств методом интервалов.
|
|
36
|
Проверочная работа.
|
|
37-40
|
Касательная к графику функции. Формула Лагранжа и её
геометрический смысл.
|
|
41
|
Приближённые вычисления.
|
|
42
|
Производная в физике и технике.
|
|
43
|
Подготовка к контрольной работе.
|
|
44-45
|
Контрольная работа №1.
|
|
46
|
Анализ контрольной работы.
|
|
Тема 3
|
Применение
производной к исследованию функций
|
|
47-50
|
Достаточный признак возрастания и убывания функции.
Теорема Дарбу.
|
|
51-53
|
Критические точки функции. Теорема Ферма (необходимое
условие экстремума). Достаточные условия экстремума функции. Теорема Ролля.
|
|
54-55
|
Выпуклость функции. Точки перегиба.
|
|
56-60
|
Исследование функции с помощью производной.
|
|
61
|
Проверочная работа.
|
|
62-67
|
Наибольшее и наименьшее значения функции. Теорема
Вейерштрасса.
|
|
68
|
Проверочная работа.
|
|
69-70
|
Повторение темы "Производная и её применения".
|
|
71-73
|
Контрольная работа №2 (итоговая за первое
полугодие).
|
|
74
|
Анализ контрольной работы
|
|
75-76
|
Теоретический зачёт по теме "Производная и
её применение"
|
|
Тема 4
|
Первообразная
|
|
77
|
Определение первообразной.
|
|
78-79
|
Основное свойство первообразной. Неопределённый интеграл.
Таблица первообразных.
|
|
80-81
|
Правила нахождения первообразных.
|
|
82-83
|
Вычисление первообразных.
|
|
84
|
Проверочная работа.
|
|
Тема 5.
|
Определённый
интеграл.
|
|
85-87
|
Площадь криволинейной трапеции.
|
|
88-89
|
Определение определённого интеграла. Формула
Ньютона-Лейбница.
|
|
90-92
|
Вычисление площадей фигур.
|
|
93
|
Проверочная работа.
|
|
94
|
Вычисление объёмов тел. Примеры применения интеграла в
физике.
|
|
95-96
|
Понятие о дифференциальных уравнениях. Решение простейших
дифференциальных уравнений. Уравнения показательного роста и показательного
убывания. Уравнение гармонических колебаний.
|
|
97
|
Контрольная работа №3.
|
|
Тема 5.
|
Задачи с
параметрами.
|
|
98-99
|
Простейшие задачи с параметрами. "Ветвление".
|
|
100-101
|
Квадратные уравнения с параметрами.
|
|
102-103
|
Квадратные неравенства с параметрами.
|
|
104-105
|
Решение задач с параметрами.
|
|
106-107
|
Графические методы.
|
|
108-109
|
Применение производной.
|
|
110-111
|
Методы поиска необходимых условий.
|
|
112
|
Контрольная работа №4.
|
|
Тема 6.
|
Основы
комбинаторики и теории вероятностей.
|
|
113
|
Правило произведения. Сочетания и размещения.
|
|
114
|
Перестановки. Решение задач.
|
|
115
|
Классическое определение вероятности.
|
|
116
|
Решение задач на определение вероятности.
|
|
117
|
Условные вероятности. Независимость событий.
|
|
118
|
Решение задач на условные вероятности.
|
|
119
|
Вероятность суммы и произведения событий.
|
|
120
|
Схема независимых испытаний.
|
|
121
|
Подготовка к контрольной работе.
|
|
122
|
Контрольная работа №5.
|
|
|
ПОВТОРЕНИЕ
|
|
123-125
|
Решение показательных уравнений, неравенств и их систем.
|
|
126-128
|
Решение логарифмических уравнений, неравенств и их систем.
|
|
129-131
|
Решение тригонометрических уравнений, неравенств и их
систем.
|
|
132-134
|
Решение иррациональных уравнений, неравенств и их систем.
|
|
135-137
|
Решение уравнений, неравенств и их систем.
|
|
138
|
Проверочная работа.
|
|
139-141
|
Производная и её применение.
|
|
142-143
|
Первообразная и интеграл.
|
|
144-146
|
Решение текстовых задач.
|
|
147-149
|
Контрольная работа №6 (итоговая за год)
|
|
150
|
Анализ контрольной работы.
|
|
151-153
|
Обобщающее повторение.
|
Преподавание геометрии в 10-11 классах идёт по учебнику
Погорелова А.В. (2 часа в неделю в 10-ом классе; 2,5 часа в неделю в
11-ом классе), в 4-ой четверти 11 класса предусмотрено повторение курса
планиметрии (10-12 уроков) с разбором конкурсных задач, предлагавшихся на
вступительных экзаменах в МГУ.
Важно, что изучение математики в химических классах
по рассматриваемой программе вызывает у учащихся искренний интерес к предмету,
желание углубить свои математические знания.
Программой предусмотрен как письменный, так и устный
контроль усвоения знаний учащимися. Как показывают результаты проверочных работ
и контрольных работ, учащиеся в своём подавляющем большинстве успешно справляются
с программой. На протяжении многих лет учащиеся успешно сдают вступительный
экзамен по математике на химический факультет МГУ и, что ещё важнее, успешно
сдают экзамены по математике, обучаясь в МГУ.
В заключение приведём по 1 варианту двух контрольных
работ:
Контрольная работа №1 (10-ый класс).
1. Решите уравнение: 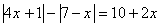
2. Решите неравенство: 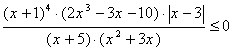
3. Решите графически уравнение: 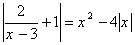
4. Решите систему уравнений: 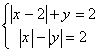 
5. При каких значениях а данное уравнение имеет 4 решения?
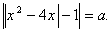
Контрольная
работа № 2 (11-ый класс).
1. Исследуйте функцию и постройте её график: 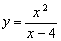 . .
2. Составьте уравнение касательной к графику функции 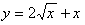 , параллельной прямой у=2х. , параллельной прямой у=2х.
3. Найдите наибольшее и наименьшее значения функции 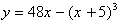 на на
отрезке [-9,5 ; -0,5].
4. Решите
неравенства методом интервалов:
а) 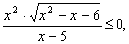 б) б) 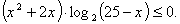
5. Бригада рыбаков отправляется на катере из пункта А вниз
по течению реки в пункт В, находящийся от А на расстоянии 144 км, а затем
поднимается против течения в пункт С, расположенный на расстоянии 81 км от
пункта В. При какой скорости течения реки время поездки будет наименьшим, если собственная скорость катера
равна 35 км/ч?
6. Напишите уравнение касательной к графику функции 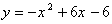 , проходящей через
точку А(4;6). , проходящей через
точку А(4;6).
Как показывают результаты анкетирования учащихся им
выпускников химических классов, изучение алгебры и начал анализа по данной
программе не приводит к их перегрузке (по данному предмету).
|

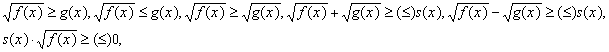 и неравенства смешанного типа.
и неравенства смешанного типа.