|
Правила приема на химический факультет МГУ
ЗАДАНИЕ ЗАОЧНОГО ТУРА
ОЛИМПИАДЫ "Абитуриент МГУ – 2004"
ХИМИЯ
1. При
определенной концентрации и температуре HNO3 реагирует с Zn с образованием
NO2 и NO в мольном соотношении NO2 : NO
= 1:3. Сколько моль HNO3 реагирует с 1 моль Zn? (1 балл).
2. В
результате серии последовательных радиоактивных распадов нуклид 235U превращается в нуклид 207Pb. Сколько a- и b-распадов
включает эта серия ядерных превращений? (1 балл).
3. Общее
количество атомов в образце предельной одноосновной карбоновой кислоты массой
97.5 г равно 13.0 моль. Определите молекулярную формулу кислоты (2 балла).
4. В молекуле алкана содержится x первичных
и y третичных
атома углерода. Найдите число четвертичных атомов углерода (2 балла).
5. Вычислите рН раствора,
полученного при смешении равных объемов 0.04 М раствора гидроксида натрия и
0.02 М раствора бромоводородной кислоты (2 балла).
6. При действии
концентрированной серной кислоты на 18.2 г твердого фторида щелочного металла
выделился газ, при пропускании которого через раствор Ca(OH)2
образовалось 27.3 г осадка. Назовите неизвестный металл. (2 балла).
7. При дегидрировании 95.0 г гомолога бензола образовался
непредельный углеводород (с одной двойной связью), который может присоединить
76.0 г брома. Напишите все возможные структурные формулы исходного
углеводорода, если выход первой реакции равен 60%, а второй - 100% (2 балла).
8. В равновесной смеси при некоторой температуре содержится
6.0 моль HI, 3.0 моль H2 и 0.8 моль I2. При охлаждении
константа равновесия H2
+ I2  2HI увеличилась в 2 раза. Рассчитайте
количества веществ в новой равновесной смеси. (3 балла). 2HI увеличилась в 2 раза. Рассчитайте
количества веществ в новой равновесной смеси. (3 балла).
9. Комплексное соединение платины содержит 50.13 мас.% Pt, 7.20 мас.% N, 41.13 мас.% Br и водород. Комплекс не
заряжен, а его молекула имеет плоское строение. Установите молекулярную формулу
комплекса и определите валентность центрального атома. Изобразите структурные
формулы двух геометрических изомеров комплекса (3 балла).
10. Напишите уравнения реакций, соответствующие следующей схеме
превращений:
C7H16NCl ← C7H15N ← C7H9N → C7H8N2O2 → C6H3N2O4K → C5H4N2O2 → C5H6N2.
В уравнениях укажите структурные формулы веществ и условия
реакций (3 балла).
11. В калориметре смешали 10.0 мл 0.50 M раствора HCl и
10.0 мл 0.50 М раствора NaOH, имеющих одинаковую температуру. Было
зафиксировано повышение температуры на DT. Оцените, как
изменится температура, если использовать 5.0 мл 0.50 M раствора NaOH вместо
10.0 мл. Считайте удельные теплоемкости обоих растворов одинаковыми (3 балла).
12. Напишите уравнения химических реакций, соответствующие
следующей схеме превращений:
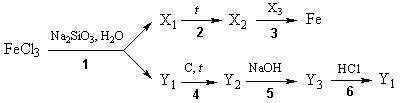
Определите неизвестные вещества (3 балла).
13. Навеску смеси гидрида бария и нитрида лития разделили
на две равные части. Одну часть растворили в воде, а вторую в избытке соляной
кислоты. Объем выделившегося газа в реакции с водой в полтора раза больше, чем
в реакции с соляной кислотой (растворимостью газов в воде пренебречь).
Определите массовую долю гидрида бария в исходной смеси (3 балла).
14. В замкнутом сосуде в молярном соотношении 1:1 при
температуре 398 K
смешали CO и Cl2. Через 5 минут
после введения катализатора давление в системе оказалось равным 2.3×105
Па, скорость образования фосгена (COCl2) в этом промежутке времени составила 2.5×10-3 моль/(л×мин). Рассчитайте
давление хлора в исходной смеси (4 балла).
15. При пропускании через 160 мл раствора, содержащего
смесь Bi(NO3)3 и
Hg(NO3)2, тока силой
0.90 А в течение 161 минуты на катоде выделилась смесь металлов общей массой
7.195 г. Напишите уравнения электролиза каждой соли и определите молярные
концентрации солей в исходном растворе, если известно, что на катоде не
выделялись газы, а после окончания электролиза раствор не содержит ионов
металлов (4 балла).
16. Оптически активный сложный
диэфир A состоит только из атомов C,
H и O. 2.81 г этого вещества подвергли омылению 30.0 мл 1.00 M раствора NaOH.
Для того чтобы полностью нейтрализовать непрореагировавший NaOH, потребовалось
6.0 мл 1.00 M раствора HCl. Продуктами омыления являются: дикарбоновая кислота B, метанол и оптически активный спирт C. В результате реакции спирта C с I2/NaOH образуются
желтый осадок и C6H5COONa. Соединение B обесцвечивает бромную воду, а при
дегидратации образует циклический ангидрид D. Изобразите структурные формулы
веществ A, B, C и D(4 балла).
17.
Получение алканов по методу Фишера-Тропша протекает на кобальтовом катализаторе
по схеме:
CO + H2  CnH2n+2 + H2O. CnH2n+2 + H2O.
Оксид углерода (II) и водород в объемном
соотношении 1:2 ввели в реакцию при 180 оС, при этом образовалась
смесь метана, этана и пропана в молярном соотношении 3:2:2. Вычислите, во
сколько раз изменилось общее давление в системе, если синтез проходил при
неизменных температуре и объеме, при этом прореагировало 10% СО (4 балла).
18. При
нагревании природного дипептида с концентрированной соляной кислотой образовались
два продукта; массовая доля хлора в одном из них составила 28.29%. При реакции
этого же дипептида с разбавленной соляной кислотой образовался продукт, в
котором массовая доля хлора равна 16.71%. Установите аминокислотный состав
дипептида, напишите для него две возможные структурные формулы (4 балла).
МАТЕМАТИКА
1.
Решить уравнение
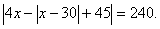 (1 балл) (1 балл)
2.
Решить неравенство
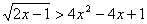 . (1 балл) . (1 балл)
3.
Решить уравнение
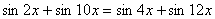 . (1 балл) . (1 балл)
4.
Решить систему уравнений
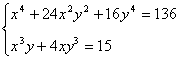 (2 балла) (2 балла)
5.
Не используя таблиц и калькуляторов, сравнить два числа
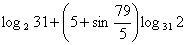 и 6. и 6.
Указание:
использовать p
= 3.14:. (2 балла).
6.
Найти площадь области на координатной плоскости, заданной
системой неравенств:
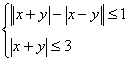 (2 балла) (2 балла)
7.
В трапеции EFGH
основания FG и EH. Известно, что ÐEFG = 90o. Проведена прямая MN, пересекающая стороны EF и GH соответственно в точках M и N, причем прямая MN перпендикулярна
стороне GH.
Известно, что HM
= 5, EN = 4, а
расстояние от точки H
до прямой MG
равно 4. Найти расстояние от точки E до прямой FN. (3 балла).
8.
Решить в целых числах x, y
и z уравнение:
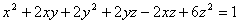 (3 балла) (3 балла)
9.
Дана замкнутая пространственная ломаная. Некоторая плоскость
пересекает все ее звенья: A1A2 в точке B1 (B1¹
A1, B1¹
A2); A2A3 в точке B2 (B2¹
A2, B2¹
A3);
:; AnA1
в точке Bn
(Bn¹
An, Bn¹
A1).
Вычислить
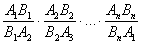 (3 балла) (3 балла)
10. Решить
уравнение
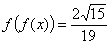 , ,
где 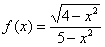 . (4 балла). . (4 балла).
11.
В четырехугольнике ABCD опущены перпендикуляры AA1, CC1 на диагональ BD и перпендикуляры BB1, DD1 на
диагональ AC.
Через O
обозначена точка пересечения диагоналей BD и AC.
Известно, что ÐAOB = p/3 и
периметр четырехугольника ABCD
равен 6. Найти периметр A1B1C1D1. (4 балла).
12.
Даны три уравнения с действительными коэффициентами:
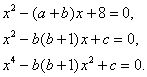
Каждое из
них имеет по крайней мере один действительный корень. Известно, что корни первого
уравнения больше единицы. Известно также, что все корни первого уравнения являются
корнями третьего уравнения и хотя бы один корень первого уравнения
удовлетворяет второму уравнению. Найти числа a, b, c, если b > 3. (4 балла).
ФИЗИКА
1.
Шайба массой m = 1.2 кг лежит на конце доски длиной l = 1.5 м, противоположный конец
которой выступает на h
= 0.5 м за край стола. Масса доски М = 2.4 кг, коэффициент трения между
доской и шайбой m
= 0.4, относительно стола доска не проскальзывает. Какую минимальную скорость V0 нужно
сообщить шайбе в направлении к краю стола, чтобы доска опрокинулась? (1 балл)
2.
Протон, пролетая мимо первоначально покоившегося ядра
неизвестного химического элемента, отклонился на угол a (cosa =
4/15), потеряв 10%
своей скорости. Найти массовое число химического элемента. (2 балла).
3.
Лыжница съезжает без начальной скорости, не отталкиваясь
палками, с горки по прямой, составляющей угол a = 60° с
горизонтальной плоскостью, и проехав расстояние l, останавливается увязнув в снегу.
Условия движения таковы, что сила сопротивления, действующая на лыжи со стороны
снега, пропорциональна пройденному к данному моменту расстоянию. Найти l, если известно, что
максимальная скорость, достигнутая лыжницей при спуске, V= 4 м/с.
(3 балла).
4.
В кубическом сосуде, сделанном из идеально упругого материала,
хаотически движутся молекулы со средней скоростью теплового движения V. Концентрация молекул n, масса каждой молекулы m. Найти давление на
стенку сосуда. (1 балл)
5.
У переменного конденсатора обкладки состоят из двух пар
соприкасающихся полудисков одинакового радиуса R. Подвижные полудиски верхней и
нижней обкладок вращаются с угловой скоростью w, то полностью перекрывая
неподвижные, то образуя с ними полные диски. Конденсатор помещён во внешнее
электрическое поле напряжённостью E, перпендикулярное к обкладкам. Конденсатор замкнут проводом
с нулевым сопротивлением. Какой ток идёт через провод? Зазор между обкладками
мал по сравнению с их радиусом. (4 балла).
6.
Из однородной проволоки, обладающей заметным сопротивлением,
сделан прямоугольник размером a´b. Перпендикулярно
плоскости прямоугольника создаётся магнитное поле, индукция которого В
линейно растёт по закону В = at.
На расстоянии с от одной из сторон длиной а подключён вольтметр,
сопротивление которого очень велико. Какое напряжение покажет этот вольтметр?
(4 балла).
7.
На мыльную пленку (n = 1.33) падает белый свет под углом 45°. При
какой наименьшей толщине пленки отражённые лучи будут окрашены в жёлтый цвет (l = 6×10-7
м)? (4 балла).
8.
Луч лазера, работающего на длине волны l = 665 нм, имеет угол
расходимости j
= 0.001 рад. Излучение регистрируется глазом на расстоянии L = 1.5×105 км.
Какова должна быть мощность излучения лазера, если глаз надёжно регистрирует n = 100 квантов в
секунду? Диаметр отверстия глаза принять d = 0.5 см. (1 балл).
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
1. Кузьменко Н.Е., Еремин В.В., Попков В.А. Начала химии. Современный
курс для поступающих в вузы. - М.: Экзамен, 1999 - 2003.
2. Кузьменко Н.Е., Еремин В.В., Попков В.А. Химия для школьников
старших классов и поступающих в вузы. - М.: Дрофа, 1997-2001.
3. Кузьменко Н.Е., Еремин В.В. 2500 задач по химии для школьников и
поступающих в вузы. - М.: Мир и Образование, 2003.
4. Химия: Справочные материалы / Под ред. Ю.Д.Третьякова. 4-е изд. -
М.: Просвещение, 2002.
5. Еремина Е.А., Рыжова О.Н. Краткий справочник по химии для
школьников. - М.: Мир и Образование, 2002.
6. Фримантл М. Химия в действии. В 2-х ч. - М.: Мир, 1991, 1998.
7. Химия. Большой справочник для школьников и поступающих в вузы. - М.:
Дрофа, 1999.
8. Московский университет - 2003. Справочник для поступающих в МГУ. -
М.: изд-во Моск. ун-та, 2003.
9. Кузьменко Н.Е., Еремин В.В., Чуранов С.С. Сборник конкурсных задач
по химии. - М.: Экзамен, 2001.
10. Кравцев С.В., Макаров Ю.Н., Чирский В.Г. и др. Методы решения задач
по алгебре. - М.: Экзамен, 2001.
11. Склянкин А.А., Зотеев А.В. Конкурсные задачи по физике с решениями.
- М.: Химический ф-т МГУ, 2001.
Издания для школьников
и абитуриентов
|

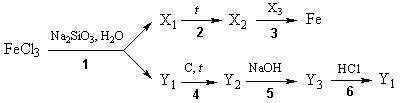
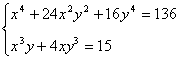 (2 балла)
(2 балла)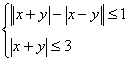 (2 балла)
(2 балла)