|
ЯДЕРНЫЙ
МАГНИТНЫЙ РЕЗОНАНС С ИМПУЛЬСНЫМ ГРАДИЕНТОМ
МАГНИТНОГО
ПОЛЯ В ИССЛЕДОВАНИЯХ СТРУКТУРЫ И
ДИФФУЗИОННОГО
ТРАНСПОРТА В ПОЛИМЕРНЫХ МЕМБРАНАХ
В.И. Волков, *В.Д. Скирда, *Е.Н. Васина,
**С.Ф.Тимашев, Б.В. Мчедлишвили
Институт кристаллографии им.А.В.Шубникова
РАН (Москва)
*Казанский государственный университет
(Казань),
**ГНЦ “НИФХИ им. Л.Я.Карпова” (Москва)
Обобщены результаты исследования самодиффузии
воды, предельных одноатомных пиртов и ионов Li+ и
F- в трековых мембранах,
имеющих регулярные калиброванные поры и в ионообменных мембранах, содержащих
сульфо-, карбоксильные, амидные и аминогруппы. Подробно обсуждаются особенности
применения метода ЯМР с импульсным градиентом магнитного поля к указанным
системам.
Трансляционная подвижность молекул при
термодинамическом равновесии (самодиффузия) является важнейшей характеристикой
физико-химического состояния любой молекулярной системы. В связи с интенсивным
развитием экспериментальных методов исследования динамики молекул, таких,
как нейтронное рассеяние, релеевское рассеяние света, ядерный магнитный
резонанс (ЯМР), большой интерес представляет изучение процессов диффузии
в сложных системам, к которым можно
отнести и полимерные мембраны. Возросший в последние годы интерес к исследованию
трансляционной динамики молекул обусловлен также существенным развитием
метода ЯМР с импульсным градиентом магнитного поля (ЯМР ИГМП), предложенным
еще в 1965г. [1].
В настоящем кратком обзоре демонстрируются
лишь некоторые, наиболее характерные, возможности метода ЯМР ИГМП и результаты
его применения, полученные авторами в течение ряда лет при исследовании
физико-химических процессов в мембранах различного типа.
Применение метода ЯМР с ИГМП к исследованию
трансляционной динамики молекул заключено в регистрации потери фазовой
когерентности спинов за счет их трансляционных перемещений в градиенте
магнитного поля. Информацию о диффузионном процессе в методе ЯМР с градиентом
магнитного поля получают из анализа диффузионного затухания 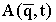 -
зависимости амплитуды сигнала спинового эхо от параметров градиента магнитного
поля и времени t.
Величина -
зависимости амплитуды сигнала спинового эхо от параметров градиента магнитного
поля и времени t.
Величина 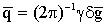 (g
- гиромагнитное отношение резонирующих ядер) непосредственно связана с
амплитудой (g
- гиромагнитное отношение резонирующих ядер) непосредственно связана с
амплитудой 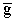 и
длительностью d
действия градиента магнитного поля и является аналогом волнового вектора,
например, в методах нейтронного рассеяния. Таким образом, диффузионное
затухание и
длительностью d
действия градиента магнитного поля и является аналогом волнового вектора,
например, в методах нейтронного рассеяния. Таким образом, диффузионное
затухание 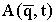 может
быть представлено динамической корреляционной функцией Ван-Хова может
быть представлено динамической корреляционной функцией Ван-Хова
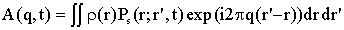 , (1) , (1)
где r
(r) - начальная плотность
спинов, Ps(r;r',t)
- плотность условной вероятности или "пропагатор" обнаружения спина при
радиус-векторе r'
в момент времени t,
если в начальный момент времени спин находился при радиусе r.
Непосредственная связь между Ps(r;r',t)
и 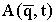 предопределяет
широкие возможности методики. Для простого случая свободной диффузии в
однокомпонентной системе и времени, отличном от микроскопического, Ps(r;r',t)
имеет вид функции Гаусса предопределяет
широкие возможности методики. Для простого случая свободной диффузии в
однокомпонентной системе и времени, отличном от микроскопического, Ps(r;r',t)
имеет вид функции Гаусса
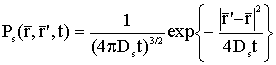 , (1a) , (1a)
со среднеквадратичным отклонением 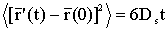 и
параметром Ds
- коэффициентом самодиффузии (КСД) [2]. и
параметром Ds
- коэффициентом самодиффузии (КСД) [2].
Таким образом, для однофазной
(с точки зрения ЯМР) системы, характеризующейся одним значением Ds,
диффузионное затухание в наиболее широко используемой последовательности
стимулированного спинового эха (рис.1) при условии
d g>
> t go
(go - постоянный
градиент магнитного поля) записывается
в виде
A(2t , t
1, g2) = A(2t , t
1,0) exp(- g 2g2d2Dstd).
(2)
Для случая экспоненциальной релаксации
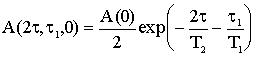 ,
(2а) ,
(2а)
где A(0)
- начальная амплитуда сигнала свободной индукции после первого 90о
– го импульса; T2
- время спин-спиновой релаксации; T1
- время спин-решеточной релаксации; t
и t 1
- временные интервалы между первым и вторым, и вторым и третьим 900–ми
р/ч импульсами, соответственно; D
- интервал между импульсами градиента; td
= (D - d /3)
- время диффузии.
Для таких простых систем не принципиально,
какой из параметров импульсной последовательности является переменным:
D ,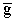 или d. Разрешающая
способность метода определяется величиной
или d. Разрешающая
способность метода определяется величиной 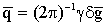 .
Получение больших градиентов магнитного поля сопряжено с серьезными техническими
проблемами. Тем не менее, если в 80-е г.г. максимальное значение .
Получение больших градиентов магнитного поля сопряжено с серьезными техническими
проблемами. Тем не менее, если в 80-е г.г. максимальное значение 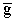 в
импульсных методиках не превышало 10 Тл/м, то к настоящему времени в некоторых
научных группах получены градиенты магнитного поля порядка 100 Тл/м и выше,
что позволяет регистрировать трансляционные смещения меньше 1000 ангстрем.
Этот успех существенно расширяет возможности метода и диапазон его приложений. в
импульсных методиках не превышало 10 Тл/м, то к настоящему времени в некоторых
научных группах получены градиенты магнитного поля порядка 100 Тл/м и выше,
что позволяет регистрировать трансляционные смещения меньше 1000 ангстрем.
Этот успех существенно расширяет возможности метода и диапазон его приложений.
Простые объекты, строго описывающиеся соотношением
(2), являются скорее исключением, чем правилом. В то же время, примеров
многофазных с точки зрения ЯМР (под “фазами” понимаются не обязательно
фазы термодинамические, поэтому здесь и ниже термин “фаза” заключен в кавычки)
молекулярных систем бесчисленное множество. В таких системах, характеризующихся
набором времен релаксации и коэффициентов самодиффузии, (если диффузионный
“пропагатор” каждой фазы подчиняется (1а)), диффузионное затухание
(ДЗ) может быть представлено суммой экспоненциальных
составляющих [2]:
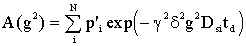 , (3) , (3)
где кажущаяся населенность p'i
определяется как
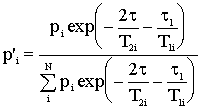 ,
(3а) ,
(3а)
N - число фаз, pi
- истинная населенность (доля) резонирующих ядер, характеризующаяся параметрами
T2i, T1i
и Dsi.
Не трудно видеть, что эксперимент должен проводиться таким образом, чтобы
временные параметры t
и t 1
были постоянными. Это возможно, если ДЗ получают путем варьирования величины
градиента магнитного поля 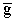 или,
реже, - длительности импульсов градиента d.
В частности, по этой причине в дальнейшем под диффузионным затуханием мы
будем понимать зависимость амплитуды сигнала спинового эхо от величины
градиента магнитного поля (A(g2)).
При этом предполагается, что все остальные параметры эксперимента выбираются
постоянными. или,
реже, - длительности импульсов градиента d.
В частности, по этой причине в дальнейшем под диффузионным затуханием мы
будем понимать зависимость амплитуды сигнала спинового эхо от величины
градиента магнитного поля (A(g2)).
При этом предполагается, что все остальные параметры эксперимента выбираются
постоянными.
Часто, в силу недостаточных возможностей
аппаратуры и сложности объекта, анализируют усредненную характеристику
- средний коэффициент самодиффузии (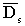 ).
Он однозначно определяется по начальному наклону диффузионного затухания
и для (3) будет равен ).
Он однозначно определяется по начальному наклону диффузионного затухания
и для (3) будет равен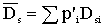 . .
Следует вновь обратить внимание на то,
что в общем случае доли p'i
кажущиеся и зависят от временных параметров эксперимента в соответствии
с (3а).
В целом, возможность получать информацию
о поведении всех молекулярных компонент многофазной системы представляется
замечательным свойством метода, определяющим его информативность. Тем не
менее, учитывая (3а), необходимо всегда достаточно осторожно интерпретировать
получаемые результаты. Действительно, для обычной последовательности стимулированного
спинового эха форма диффузионного затухания будет функцией времени диффузии,
поскольку изменение td
в (3) связано с интервалом t 1
в (3а), а это ведет к кажущейся зависимости от td
населенностей p'i.
Один из способов учета такого нежелательного эффекта заключается в перенормировке
результатов диффузионных исследований по данным дополнительных измерений
ядерной релаксации. Более достоверная информация о зависимости характеристик
трансляционной динамики молекул от времени диффузии может быть получена,
если использовать специальную пяти-импульсную последовательность, позволяющую
варьировать время диффузии при постоянных временных параметрах для ЯМ-релаксации.
Подробно проблемы учета ядерной релаксации рассмотрены в [2].
Для многофазных систем всегда корректен
вопрос о природе отдельных “фаз” (компонент) и о взаимодействии между ними.
Часто равновесие между “фазами” контролируется процессами обмена. Исследование
характеристик обмена является одной из фундаментальных задач физической
химии.
Впервые задача измерения коэффициентов
самодиффузии при наличии обмена между фазами была рассмотрена в [3] на
примере двухфазной системы в предположении экспоненциальных функций распределения
времен жизни в “фазах”. В [2] был рассмотрен более общий случай. Для условий
медленного и быстрого обменов результаты совпадают. В условиях медленного
обмена диффузионное затухание описывается выражением (3), а при быстром
обмене 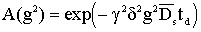 .
Наиболее интересна ситуация в условиях промежуточного обмена. Например,
даже для двухфазной системы (“фазы” a
и b) форма диффузионного
затухания описывается непрерывным спектром коэффициентов самодиффузии.
Главный результат состоит в том, что крайние значения этого спектра вполне
однозначно определены величинами Dsa
и Dsb,
а населенности pa и
pb
этих компонент есть убывающие функции времени диффузии td: .
Наиболее интересна ситуация в условиях промежуточного обмена. Например,
даже для двухфазной системы (“фазы” a
и b) форма диффузионного
затухания описывается непрерывным спектром коэффициентов самодиффузии.
Главный результат состоит в том, что крайние значения этого спектра вполне
однозначно определены величинами Dsa
и Dsb,
а населенности pa и
pb
этих компонент есть убывающие функции времени диффузии td:
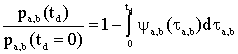 , ,
где pa,b
(td = 0) - истинная населенность
“фазы” a или b,
а интеграл - накопленная за время td
вероятность покинуть соответствующую “фазу” хотя бы один раз.
Таким образом, анализ зависимостей pa,b(td)
дает принципиальную возможность определить вид функции Y
( t )
распределения времени жизни в фазах, а по ней легко найти среднее время
жизни в “фазе”. Наиболее просто поддается анализу населенность “фазы” с
наименьшим коэффициентом самодиффузии. Одним из важнейших критериев обмена
является независимость среднего коэффициента самодиффузии от времени диффузии.
При рассмотрении поведения среднего КСД
жидкости в пористой структуре можно выделить три основных временных режима:
-
коротковременной режим - когда среднеквадратичные
смещения молекул жидкости меньше линейных размеров пор и существенного
влияния поверхности пор на измеряемый коэффициент самодиффузии не наблюдается:
D* » D,
где D -
коэффициент самодиффузии объемной жидкости;
-
режим промежуточных времен диффузии, когда
среднеквадратичные смещения молекул жидкости сравнимы с размерами пор.
В этом режиме эффективный коэффициент D*
зависит от времени диффузии;
-
длинновременной режим. Здесь ситуация определяется
конкретной структурой пористого пространства.
В случае замкнутых пор в длинновременном режиме
можно наблюдать признак полностью ограниченной диффузии, а именно: D*Ґ
t-1. Из данных этого
режима можно извлечь параметры линейных размеров ограничений, используя
соотношение Эйнштейна 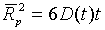 . .
В случае связанных пор в длинновременном
режиме среднеквадратичные смещения молекул жидкости больше размеров пор,
и движение жидкости оказывается усредненным по пространству системы. В
этом случае для пористых систем со случайной структурой диффузионные затухания,
как правило, экспоненциальны и характеризуются эффективным КСД, не зависящим
от времени диффузии.
Таким образом, поведение среднего КСД молекул
в системе ограничений определяется тремя слагаемыми: КСД чистой жидкости,
самим эффектом ограничений и эффектом проницаемости. В работе [4] для корректного
разделения указанных эффектов преложены скейлинговые выражения, позволяющие
получить информацию о размерах ограничений (характеристике пористой среды)
по полному анализу всей зависимости КСД от времени диффузии, включающей
все три основных режима.
Для системы связанных пор с пространственной
периодичностью ожидаемая форма диффузионных затуханий в длинновременном
режиме существенно отличается от экспоненты и характеризуется отчетливо
наблюдаемым эффектом “диффузионной” дифракции [5,6].
Анализ формы диффузионных затуханий (ДЗ)
усложняется, когда для всех или одной из “фаз” “пропагатор” оказывается
негауссовым. Типичные для этого случая системы - это системы с пространственными
ограничениями.
Самодиффузия в системе изолированных пор
впервые рассматривалась в работе Стейскала и Таннера [6]. Для равноудаленных
на расстояние a
параллельных плоскостей при направлении 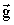 вдоль
нормали к ним выражение для ДЗ имеет вид вдоль
нормали к ним выражение для ДЗ имеет вид
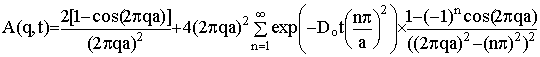 (4) (4)
где аналог волнового вектора q=g
d g/2p (g
- гиромагнитное отношение резонирующих ядер, g
и d - амплитуда
и длительность градиентных импульсов, Dо
- КСД объемного диффузанта, t
- время диффузии). В литературе неоднократно приводились ДЗ, рассчитанные
по выражению (4), однако динамический диапазон изменения амплитуды сигнала
в них оказался недостаточным для корректного сравнения с нашими данными.
Кроме того, оказалось важным сравнивать вид затуханий ДЗ, полученных при
определенном сочетании параметров g, d
и t. На
рис.2 показаны ДЗ, рассчитанные по выражению
(4) для разных t при
td 2=const.
Эффективный КСД D*,
извлекаемый из наклона касательной к начальному участку ДЗ, определяется
величиной среднеквадратичных смещений молекул за время t при любом виде
“пропагатора” [2].
В коротковременной области (кривые 1 и
2) ДЗ имеют вид, типичный для многофазной системы: их можно описать суммой
(3), а версии о негауссовом “пропагаторе” и “многофазности” системы оказываются
неразличимыми. В работах [7,8] отмечалось, что конечный участок ДЗ с негауссовым
“пропагатором” соответствует той части молекул, которая испытала влияние
ограничений: для этих молекул произошли нарушения в гауссовом распределении
смещений. В то же время, для
молекул, находящихся вдали от отражающей стенки, наблюдается режим свободной
диффузии с Do
и экспоненциальной компонентой в ДЗ. Таким образом, ансамбль молекул можно
разделить на две условные “фазы”: свободные молекулы и молекулы, испытавшие
влияние ограничений.
Амплитуда ДЗ на конечных участках (кривые
1 и 2 на рис.2) при одинаковых g
пропорциональна 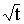 .
Это обусловлено тем, что толщина слоя молекул, испытавших влияние ограничений,
контролируется диффузионным процессом и пропорциональна .
Это обусловлено тем, что толщина слоя молекул, испытавших влияние ограничений,
контролируется диффузионным процессом и пропорциональна 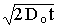 . .
В пределах изменения амплитуды сигнала
от 1 до примерно 0,1 ДЗ на рис.2 можно описать
экспонентой с эффективным КСД D*,
зависящим от t.
Этот факт позволяет заключить, что ДЗ “многофазной” системы при наличии
“негауссовости” можно описать выражением (3), в котором компоненты с негауссовым
“пропагатором” представляются в виде экспонент с Dsi=D*si(t),
где D*si(t)
- эффективные КСД “фаз” с негауссовым “пропагатором”.
Анализ экспериментальных результатов, полученных
при ориентации 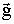 вдоль
плоскости пленок трековых мембран (ТМ) с пористостью 3% и диаметрами пор
0,9мкм (при a =90°
, где a
- угол между нормалью к плоскости мембраны и вектором градиента магнитного
поля) для системы, насыщенной водой, показал следующее. вдоль
плоскости пленок трековых мембран (ТМ) с пористостью 3% и диаметрами пор
0,9мкм (при a =90°
, где a
- угол между нормалью к плоскости мембраны и вектором градиента магнитного
поля) для системы, насыщенной водой, показал следующее.
ДЗ (рис.3)
при временах диффузии от трех (минимальное в эксперименте) до 15мс представляли
собой сумму двух основных “фаз”.
Первая “фаза” (около 60% сигнала) характеризовалась
КСД Dsb,
не зависящим от t и равным КСД объемной воды; эта “фаза” соответствовала
молекулам воды между пленками ТМ. Другая “фаза” характеризовалась КСД Dsa,
минимальным из спектра, полученного при формальном разложении ДЗ по выражению
(2); в качестве Dsa»
10-12м2/c
выступали эффективные КСД молекул воды в порах, причем для этих молекул
выполнялся режим полностью ограниченной диффузии DsaҐ
t-1. Общая доля промежуточных
компонент (между компонентами с Dsa
и Dsb)
составляла 35%.
Появление промежуточных Dsi
связано с возможностью диффузионного молекулярного обмена между каналами
пор и областью свободной диффузии. Для нахождения функции распределения
времен жизни молекул воды в порах (в “фазе” с наименьшим КСД) мы использовали
известную методику, предложенную в [2], которая применялась для случая
пористых систем в [4]. Общее выражение для вероятности пребывания молекул
в фазе a в течение
времени t имеет
вид 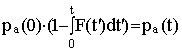 , где
F(t') - искомая
функция распределения времен жизни, pa(t)
- населенность компоненты с наименьшим КСД, , где
F(t') - искомая
функция распределения времен жизни, pa(t)
- населенность компоненты с наименьшим КСД, 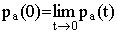 [2]. Полученная
из экспериментальных данных F(t)
представлена на рис.4, там же представлена F(t),
рассчитанная по выражению [2]. Полученная
из экспериментальных данных F(t)
представлена на рис.4, там же представлена F(t),
рассчитанная по выражению
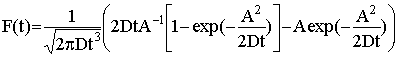 (5) (5)
(где A
- расстояние между границами), полученному в [8] при решении одномерной
задачи о первом достижении границ, когда оно осуществляется диффузионным
способом.
Рис.4 демонстрирует
прекрасное совпадение экспериментальных и расчетных данных и подтверждает
правомерность подхода в терминах диффузионного молекулярного обмена. Среднее
время жизни молекул воды в порах, 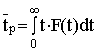 ,
оказалось равным 5±
0,5мс. ,
оказалось равным 5±
0,5мс.
ДЗ, полученные в диапазоне t
от 3 до 9мс при a =0°
, имели вид, подобный ДЗ для a
=90° .
Форма ДЗ удовлетворяла признакам “двухфазной” системы: одна “фаза” характеризовала
свободную диффузию воды в порах; другая фаза (с наименьшим КСД Dsa,
для которого DsaҐ
t-1) - ограниченную самодиффузию
воды между поверхностями соседних трековых мембран. Т.е., по сравнению
со случаем a =90°
, произошла “инверсия” качественного
состояния “фаз”. Оценка толщины слоя воды между поверхностями пленок составила
0,5± 0,1мкм,
а среднее время жизни молекул воды между пленками 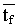 -
3 - 4мс. Населенность полностью ограниченной фазы (с Dsa)
оказалась примерно вдвое меньшей таковой для a
=90° .
Сумму -
3 - 4мс. Населенность полностью ограниченной фазы (с Dsa)
оказалась примерно вдвое меньшей таковой для a
=90° .
Сумму 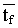 + +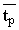 можно трактовать как среднее время нахождения молекул воды в пределах одного
слоя пленки.
можно трактовать как среднее время нахождения молекул воды в пределах одного
слоя пленки.
Периодическая структура системы была образована
параллельно сложенными пленками; наименьшее время прохождения периода системы
можно определить суммой 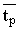 + +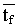 .
При a =0°
и t>10мс
(> .
При a =0°
и t>10мс
(>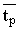 + +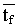 )
на ДЗ наблюдались “биения” - эффект “диффузионной дифракции” [9]. Период
пористой системы, определяемый обратной величиной волнового вектора q в
точке максимума на ДЗ [9], был равен 10,6±
0,2мкм и соответствовал сумме толщины пленки ТМ и среднего расстояния между
соседними ТМ. Эффект “диффузионной дифракции” можно использовать в качестве
теста на наличие проницаемости пленочных мембран по отношению к молекулам
диффузанта. )
на ДЗ наблюдались “биения” - эффект “диффузионной дифракции” [9]. Период
пористой системы, определяемый обратной величиной волнового вектора q в
точке максимума на ДЗ [9], был равен 10,6±
0,2мкм и соответствовал сумме толщины пленки ТМ и среднего расстояния между
соседними ТМ. Эффект “диффузионной дифракции” можно использовать в качестве
теста на наличие проницаемости пленочных мембран по отношению к молекулам
диффузанта.
На рис.5
представлена угловая зависимость населенности компоненты ДЗ с КСД равным
2,68 10-11м2/c
(наименьший КСД при a =90°
, соответствующий молекулам воды в
порах трековой мембраны, когда каналы пор строго перпендикулярны поверхности
пленки) от a
. Представленные данные демонстрируют появление минимума (примерно при
a =40о),
и это означает, что угловое распределение каналов пор от нормали к поверхности
пленки составляет примерно 40о.
В таблице 1 представлены данные оценок
диаметров пор трековых мембран, полученные при a
=90° для
разных диффузантов и трековых мембран.
Таблица 1
Диаметры пор ТМ, полученные
по данным самодиффузии при a =90°
|
Диффузанты |
Средний диаметр пор ТМ (мкм) по данным
эл. микроскопии
|
Диаметры пор ТМ (мкм), полученные
из данных самодиффузии
|
| Вода |
1,2 - 1,3
|
1,8± 0,02
|
| 1,3-пропиленгликоль |
0,2 - 0,25
|
0,26± 0,01
|
| ПДМС
2.000 |
1,2 - 1,3
|
1,8± 0,02
|
Одной из важных и интересных областей применения
метода ЯМР ИГМП являются ионообменные мембраны. В этих системах функциональные
группы, молекулы воды и подвижные ионы организуют сеть транспортных каналов
для избирательного переноса ионов и молекул [10,11]. Выявление механизмов
ионного и молекулярного транспорта - одна из основных научных проблем мембранного
разделения. Решение данной проблемы требует установления взаимосвязи между
структурой транспортных каналов, степенью взаимодействия диффузант - функциональная
группа и трансляционной подвижностью ионов и молекул [11].
Проанализируем основные факторы, определяющие
ионный и молекулярный транспорт.
Влияние геометрии транспортных каналов
на самодиффузию наиболее ярко проявляется при сопоставлении перфторированных
сульфокатионо-обменных мембран (ПСМ) и ионообменников на основе стирола
с дивинилбензолом (МК-40, КУ-2). В перфторированных мембранах транспортные
каналы занимают около четверти объема и имеют довольно регулярную структуру
(ширина канала около 5 нм) [10]. По этой причине перенос диффузанта складывается
из множества трансляционных перескоков частиц между сульфогруппами, перескоков,
происходящих с близкими частотами [12,13]. В отличие от ПСМ в МК-40 и КУ-2
сульфогруппы образуют сеть последовательно соединенных кластеров и каналов.
Основная доля сульфогрупп, а следовательно катионов металлов и молекул
воды, находится в кластерах, где катионы и молекулы воды имеют высокую
подвижность. Каналы образованы одиночными сульфогруппами, и подвижность
ионов и молекул воды в каналах значительно ниже, чем в кластерах [11,14,15].
При этом лимитирующей стадией диффузионного транспорта ионов и молекул
является перенос частиц в межкластерном канале.
Регулярность в расположении функциональных
групп в ПСМ по сравнению с КУ-2 и МК приводит к тому, что селективность
и транспортные свойства ПСМ существенно лучше, чем КУ-2 и МК. Очевидно,
это обусловлено тем, что, именно благодаря такой регулярности, в перфторированных
мембранах могут быть контролируемым образом реализованы остальные факторы
избирательного диффузионного переноса, к которым прежде всего нужно отнести
взаимодействие диффузант - функциональная группа.
Определяющую роль в этом взаимодействии
играют процессы гидратации (сольватации). Было установлено, что молекулы
воды взаимодействуют преимущественно с катионами металлов, которые разрушают
сетку водородных связей между молекулами воды и структурируют ее. Индивидуальность
иона металла в структурировании воды в канале проявляется наиболее ярко
при n < ho
, где n - количество молекул воды, приходящихся на ионную пару сульфогруппа-катион,
ho
- максимальное число гидратации катиона [16]. В этих условиях катион металла
непосредственно связан с сульфогруппой и образуется контактная ионная пара.
Это обстоятельство приводит к следующим особенностям процесса самодиффузии
воды и ионов в мембранах при низких влагосодержаниях:
Трансляционная подвижность
воды уменьшается по мере роста гидратирующей способности катиона, как это
видно из рис. 6. На этом рисунке сопоставлены
коэффициенты самодиффузии и протонные химические сдвиги воды; химические
сдвиги характеризуют взаимодействие катион-вода [16]. Важно отметить, что
эти данные получены при одних и тех же n=2,5 , что меньше ho
, которое минимально для иона Cs+ (ho
=3,0 [16]). Кроме этого, при фиксированных значениях n геометрические размеры
каналов примерно одинаковы для разных ионных форм мембран. Все это позволяет
нам достаточно корректно выявить влияние взаимодействия вода-катион на
самодиффузию воды.
Трансляционные перемещения
воды и ионов скоррелированы между собой. Так, при уменьшении влагосодержания
коэффициенты самодиффузии ионов Li+
и воды сближаются и их зависимости от n носят одинаковый характер (рис.
7) [17], а коэффициенты самодиффузии ионов F-
и молекул воды в анионообменных мембранах практически совпадают [18].
Для гидратации воды в
ионных каналах мембран при n < ho
характерно также отсутствие фазового перехода в области 0o
С - кривая 1 рис. 8 [12,13].
Очевидно, что в данных условиях водородные
связи между молекулами воды разрушены настолько, что создать для них дальний
порядок невозможно. Другой причиной сохранения высокой подвижности воды
при температуре ниже 0o
С могут быть стерические препятствия для создания структуры льда из-за
малой ширины транспортных каналов [19]. Таким образом, в области n Ј
ho основной
вклад в диффузионный перенос дает энтропийная составляющая, для которой,
исходя из представлений теории протекания, было получено следующее выражение:
D = Do exp(p(a-
n1/3)m ), (6)
где p
и m характеризуют
вероятность перескока молекул воды и ионов между смежными функциональными
группами, а параметр a
определяет плотность упаковки молекул воды в гидратной оболочке противоиона
[10]. Как видно из рис. 7, соотношение (6) хорошо
описывает зависимость от влагосодержания коэффициентов самодиффузии воды
и ионов Li+ в Li+-форме
ПСМ. Перкаляционная модель позволяет также предсказать изменение коэффициентов
самодиффузии при варьировании структуры транспортных каналов в процессе
синтеза мембран. Так, увеличение концентрации сульфогрупп в ПСМ сопровождалось
резким возрастанием коэффициентов самодиффузии воды, к тому же результату
приводило введение дополнительных центров гидратации в виде амидных групп
в моносульфосодержащих ароматических полиамидах ПА-1 [20]. В обоих случаях
уменьшалось расстояние между смежными функциональными группами и увеличивалась
вероятность трансляционного перескока молекул от группы к группе, что сопровождалось
ростом коэффициента самодиффузии.
Увеличение влагосодержания мембран приводило
к образованию следующих гидратных оболочек ионов и, соответственно, к разрыву
контактных ионных пар. В этом случае самодиффузия воды и ионов в мембранах
была во многом аналогична их самодиффузии в водных растворах электролитов.
Представляется интересным рассмотреть самодиффузию
воды в мембранах различного типа в областях температур выше и ниже 0o
С при n і ho
. Здесь возможны две ситуации. Первая: вода по-прежнему является связанной,
и доля подвижной воды не изменяется при переходе через 0o
С, однако ниже 0o С
вода находится в более ассоциированном состоянии, и энергия активации самодиффузии
воды выше, чем в области положительных температур - кривые 2, 2ў
на рис. 8 [12]. Вторая ситуация характерна прежде
всего для систем с неоднородной структурой транспортных каналов, типичный
пример представлен кривыми 3 и 3ў
на рис. 8, изображающими соответственно температурные
зависимости коэффициентов самодиффузии и количества подвижной воды в макропористом
сульфокатионите КУ-23 [14,15]. Очевидно, что при понижении температуры
основная часть воды, расположенной в макропорах, замерзает, а вода, находящаяся
в узких ионогенных каналах, сохраняет высокую подвижность при низких температурах,
и ее самодиффузия характеризуется большой энергией активации. Таким образом,
анализ температурных зависимостей коэффициентов самодиффузии и интенсивности
сигнала спинового эха (пропорциональной количеству подвижных молекул воды)
весьма полезен. Заметим, что метод ЯМР ИГМП удачно
дополняет калориметрические методы. Так, с помощью метода ДСК наблюдали
переход в области 0o
С не только во втором, но и в первом случае, когда, по данным ЯМР, вся
вода оставалась подвижной ниже 0o
С.
В связи с важностью процессов разделения
водно-органических смесей на мембранах с катионообменными группами интересно
рассмотреть самодиффузию органических молекул в мембранах. На
рис. 9 приведены зависимости коэффициентов самодиффузии
воды, метанола, этанола и пропанола от содержания данных диффузантов в
ПСМ. Видно, что эти зависимости имеют одинаковый характер. Было установлено,
что самодиффузия спиртов в ионогенных каналах во многом аналогична самодиффузии
воды, однако, в отличие от воды, молекулы спирта могут внедряться в гидрофобную
часть матрицы. В области больших n коэффициенты самодиффузии уменьшаются
в ряду вода - метанол - этанол - пропанол - бутанол в той же последовательности,
что и коэффициенты самодиффузии объемных жидкостей. При малых n трансляционная
подвижность метанола и этанола больше по сравнению с водой (рис.
9) [21]. Таким образом, как и в случае разделения ионов, варьируя n,
можно регулировать степень разделения вода - органическая фракция.
Установленные закономерности характерны
для широкого класса мембран и сорбентов. В частности, нами исследовались
перфторированные карбоксилсодержащие мембраны, ионообменные смолы на стиролдивинилбензольной
основе КУ-2, КУ-23, АВ-17 и мембраны МК; пленки ароматических моно-
(ПА-1) и бисульфосодержащих (ПА-2) полиамидов
[11,20,]; пленки пространственно сшитых полиакриловых кислот [22]; ацетатцеллюлозные
мембраны [19]. Эти системы различаются морфологией транспортных путей и
химической природой функциональных групп, включенных в
каналы.
Особенностью перечисленных систем является
то обстоятельство, что в них невозможно независимо изменять структуру транспортных
каналов и степень взаимодействия диффузант - полимерная матрица, что существенно
затрудняет интерпретацию эксперимента. Для более глубокого понимания природы
взаимосвязи структура – взаимодействие - самодиффузия необходимы исследования
модельных объектов. Такими объектами могут стать трековые мембраны или
ядерные фильтры, имеющие ориентированные поры заданного диаметра, который
варьируется от 10нм до 1мкм. Эти мембраны могут быть модифицированы различными
физико-химическими способами с целью изменения взаимодействия диффузант
-поровая поверхность, при неизменной структуре пор [23].
Еще одно достоинство ЯМР ИГМП заключается
в возможности измерять парциальные коэффициенты самодиффузии и растворимости
диффундирующих компонентов жидких смесей в гетерогенных мембранных системах
[11,22]. В качестве примера на рис.
10 представлена зависимость амплитуды сигнала спинового эхо от величины
градиента магнитного поля A(g) для композитной мембраны на основе полиакриловой
кислоты (ПАК), нанесенной на полисульфоновую подложку (ПСФ); мембрана была
уравновешена с водно-этанольной смесью [22]. Как видно из этого рисунка,
варьируя длительность градиентного импульса d
, можно определять относительные доли и коэффициенты самодиффузии компонентов
водно-этанольных смесей - как в пленке ПАК, так и в ультрапористой подложке
ПСФ. Исходя из этих значений, были определены факторы разделения водно-этанольных
смесей для мембран различного типа [11].
Из таблицы 2 видно, что наибольшими факторами
разделения обладают пленки пространственно сшитых бисульфосодержащих ароматических
полиамидов ПА-2 и композитные мембраны ПАК+ПСФ, в то время как в перфторированных
сульфокатионитовых мембранах ПСМ и в пленках моносульфосодержащих ароматических
полиамидов факторы разделения на порядок ниже. Этот факт обусловлен тем
обстоятельством, что в ПА-2 и ПАК+ПСФ образуются два типа транспортных
каналов для преимущественного переноса водного и органического компонентов
соответственно, а в ПСМ и ПА-1 перенос воды и этанола осуществляется в
одном и том же ионном канале [11,22].
Таблица 2
Фактор разделения водно-этанольных
смесей
для мембран различного
типа
|
Параметры
при 50oС
|
ПСМ
|
ПА-1
|
ПА-2
|
ПАК+ПСФ
|
|
DsH2O 10-10
м2/с
|
6
|
0,6
|
40
|
1,3
|
|
DsEtOH 10-10
м2/с
|
1,5
|
0,15
|
0,1
|
0,026
|
|
a s
|
12
|
15
|
25
|
16
|
|
a m
|
4
|
4
|
400
|
50
|
|
a
|
48
|
60
|
10000
|
800
|
В таблице 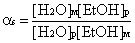 ;
a m = DsH2O/DsEtOH
; a = a sa
m. ;
a m = DsH2O/DsEtOH
; a = a sa
m.
Работа частично поддержана фондом РФФИ
(№ 97-03-32668а)
Литература
-
Steiskal E.D., Tanner J.E. // J. Chem. Phys., 1965, V. 42, No. 1, P. 288.
-
Маклаков А.И., Скирда В.Д., Фаткуллин Н.Ф.
Самодиффузия в растворах и расплавах полимеров. Казань: Изд. Каз. гос.
университета, 1987, 224с.; Maklakov A.I., Skirda V.D., Fatkullin N.F. Encycl.
of Fluid Mechanics, 1990, Chap. 22, Р. 705.
-
Karger J. // Annalen der Physik, 1969, V. 24, No. 1/2, P. 1.
-
Valiullin R.R., Skirda V.D., Stapf S., Kimmich R. // Phys. Rev. E, 1997,
V. 55. No. 3, P. 2664. Скирда В.Д., Севрюгин
В. А., Маклаков А. И. // Докл. АН СССР, 1983, Т.
-
Callaghan P.T. // Magn. Res. Imaging, 1996, V. 14, No. 7/8, P. 701.
-
Tanner J.E., Stejskal E.O. Restricted Self-Diffusion of Protons in Colloidal
Systems by the Pulsed-Gradient, Spin-Echo Method // J. Chem. Phys., 1968,
V. 49, P. 1768.
-
Hurlimann M.D., Helmer K.G., de Swiet T.M., Sen P.N., and Sotak C.H. Spin
Echoes in a Constant Gradient and in the Presence of Simple Restriction
// J. Magn. Reson., 1995, V. A113, P. 260.
-
Callaghan P.T., Codd S.L., Generalised Calculation of NMR Imaging Edge
Effects Arising from Restricted Diffusion in Porous Media // Magn. Reson.
Imaging, 1998, V. 16, P. 471-478.
-
Рытов С.М., Введение в статистическую радиофизику.
Ч. 1. Случайные процессы. - М.: Наука, 1976, 496с. Callaghan P.T., Coy
A., MacGowan D., Packer K.J., Zelaya F.O. Diffraction-like effects in NMR
diffusion studies of fluids in porous solids // Nature, 1991, V. 351, P.
467-469.
-
Тимашев С.Ф. Физикохимия мембранных процессов.
М.: Химия, 1988, 238с.
-
Волков В.И. Избирательный ионный и молекулярный
транспорт в ионообменных мембранах по данным магнитного резонанса - Автореферат
докт. дис., М., 1994.
-
Волков В.И., Нестеров И.А., Тимашев С.Ф. и
др. Химическая физика, 1989, т. 8, № 1, с. 128.
-
Волков В.И., Тимашев С.Ф. Ж..физ.химии, 1989,
т. 63, № 1, с. 69.
-
Салдадзе Г.К., Волков В.И., Тагирова Р.И.
и др. Ж.физ.химии, 1993, т. 67, № 4, с. 773.
-
Салдадзе Г.К., Тагирова Р.И., Волков В.И.
и др. Ж.физ.химии, 1993, т. 67, № 9, с. 1818.
-
Волков В.И., Сидоренкова Е.А., Тимашев С.Ф.
и др. Ж.физ.химии, 1993, т. 67, № 5, с. 1014.
-
Нестеров И.А. Особенности диффузионной подвижности
молекул воды и ионов Li+
в перфторированных сульфокатионитовых мембранах по данным импульсных методов
ЯМР - Автореферат канд. дис., М., 1986.
-
Волков В.И., Попков Ю.М., Тимашев С.Ф. и др.
Структура и динамика молекулярных систем , ч.2, Йошкар-Ола-Казань-Москва,
1998.
-
Volkov V.I., Korotchkova S.A., Nesterov I.A. etc. J.Membr.Sci., 1996, V.
110, P. 1-11.
-
Волков В.И., Корочкова С.А., Кирш Ю.Э. и др.
Ж.физ.химии., 1994, т. 68, № 7, с. 1310.
-
Волков В.И., Корочкова С.А., Тимашев С.Ф.
Ж.физ.химии., 1995, т. 69, № 6, c. 1124.
-
Volkov V.I., Korotchkova S.A., Ohya H. etc. J.Membr.Sci., 1995, V. 100,
P. 273.
-
Mchedlishvili B.V., Beryozkin V.V., Oleinikov V.A. etc. J.Membr.Sci., 1993,
V. 79, P. 285-304.
|

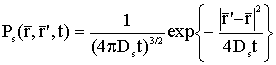 , (1a)
, (1a)
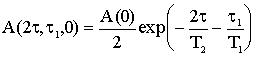 ,
(2а)
,
(2а)
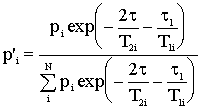 ,
(3а)
,
(3а)
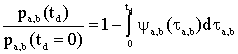 ,
,
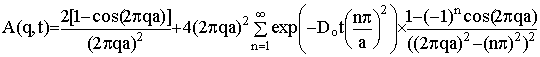 (4)
(4)
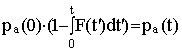 , где
F(t') - искомая
функция распределения времен жизни, pa(t)
- населенность компоненты с наименьшим КСД,
, где
F(t') - искомая
функция распределения времен жизни, pa(t)
- населенность компоненты с наименьшим КСД, 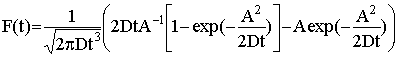 (5)
(5)
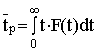 ,
оказалось равным 5±
0,5мс.
,
оказалось равным 5±
0,5мс.