 |

|
|
[ На предыдущий раздел]
4.3. Субмодели третьего иерархического уровня (С-уровня) посвящены расчету движущих сил и основных потоков, а именно, потоков массы и энергии в фазах, в слое геля, а также через мембрану.
Субмодель (С1), описывающая явление ТП. Данная субмодель предназначена для описания температурного поля и ТП, ее включение необходимо при моделировании процесса, протекающего при неизотермических условиях. Подробное описание данной субмодели представлено в работах [12–15]. Она построена на основе транспортного интеграла, описывающего продольный перенос тепла:
|
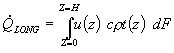 . .
|
(18) |
Транспортный интеграл (18) распадается на два слагаемых, соответствующих зонам с переменной (зона А) и с постоянной температурой (зона В):
|
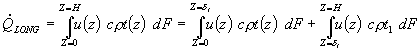 . .
|
(19) |
Для упрощения математических преобразований использованы безразмерные переменные e и h, позволяющие использовать математические формулировки для профиля скорости, u(h), и температуры, t(e), в безразмерном виде.
Перенос в зоне А. Интегрирование и последующие преобразования выражения, описывающего транспорт в пределах зоны А (см. первое слагаемое в правой части выражения 19), осуществлялось в безразмерных координатах, e:
|
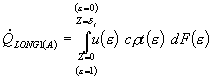 . .
|
(20) |
В результате интегрирования и последующих преобразований транспортной составляющей, описывающей перенос в зоне А, получено следующее выражение:
|
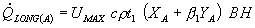 . .
|
(21) |
Промежуточные выражения X A и YA представлены в форме единичных матриц, являющихся произведением соответствующих векторов.
Перенос в зоне В. Второе слагаемое 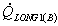 в правой части выражения (19) отражает транспорт в пределах зоны В, лежащей между верхней границей температурного слоя и осевой линией канала, где наблюдается изменение скорости, в то время как температура остается постоянной, то есть равной температуре в ядре t1: в правой части выражения (19) отражает транспорт в пределах зоны В, лежащей между верхней границей температурного слоя и осевой линией канала, где наблюдается изменение скорости, в то время как температура остается постоянной, то есть равной температуре в ядре t1:
|
 . .
|
(22) |
В результате дальнейших преобразований транспортной составляющей, описывающей перенос в зоне В, получено следующее выражение:
|
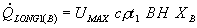 . .
|
(23) |
Выражения (21) и (23) представляют собой количественную связь между продольным транспортом тепла и параметрами температурного и гидродинамического поля, а именно, осевой скоростью, UMAX, и объемной температурой, t1. Решенные относительно степени ТП (b1), данные выражения позволяют прогнозировать изменение степени ТП по длине канала. Серия расчетных профилей степени ТП для плоскорамного мембранного модуля при различных значениях реологического индекса m показана на рис. 3. Данная субмодель дает связь между значениями температуры на поверхностях мембраны, величиной трансмембранного потока, параметрами мембраны и теплофизическими свойствами среды.
Субмодель (С2), описывающая явление КП. Данная субмодель, см. рис. 2, позволяет моделировать явление КП и прогнозировать профиль степени КП по длине канала. Подробное описание данной субмодели представлено в работах [16–18]. Она построена на основе транспортного интеграла, описывающего продольный перенос массы:
|
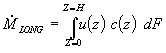 . .
|
(24) |
Для упрощения математических преобразований контрольное сечение потока подразделяется на две зоны: зона С, лежащая между Z = 0 и Z = d C, и зона D, лежащая между Z = dC и Z = Н, при этом транспортный интеграл (24) можно представить в виде суммы двух слагаемых:
|
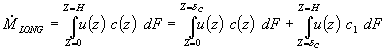 . .
|
(25) |
Перенос в зоне С. Для дальнейшего моделирования переноса в пределах зоны С 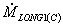 (см. первое слагаемое в правой части выражения 25) были использованы безразмерные координаты, q: (см. первое слагаемое в правой части выражения 25) были использованы безразмерные координаты, q:
|
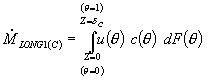 . .
|
(26) |
В результате интегрирования и последующих преобразований получено следующее выражение:
|
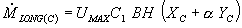 . .
|
(27) |
Промежуточные выражения XС и YС представлены в форме единичных матриц, являющихся произведением соответствующих векторов.
Перенос в зоне D. Второе слагаемое в правой части выражения (25) отражает транспорт в пределах зоны D,  , лежащей между верхней границей диффузионного слоя и осевой линией канала, где наблюдается изменение скорости, в то время как концентрация остается постоянной, равной концентрации в ядре C1: , лежащей между верхней границей диффузионного слоя и осевой линией канала, где наблюдается изменение скорости, в то время как концентрация остается постоянной, равной концентрации в ядре C1:
|
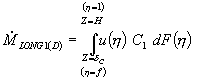 . .
|
(28) |
В результате интегрирования получено следующее выражение:
|
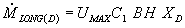 . .
|
(29) |
Выражения (27) и (29) представляют собой количественную связь между продольным транспортом массы и параметрами концентрационного и гидродинамического поля. Выражения (27) и (29), решенные относительно степени КП (a), позволяют количественно прогнозировать изменение степени КП по длине канала. Серия расчетных профилей степени КП для плоскорамного мембранного модуля показана на рис. 4.
Данная субмодель содержит также блок уравнений, описывающих концентрационное поле в процессах микрофильтрации для более сложных случаев, когда коэффициент диффузии является функцией скорости деформации [11]. В основе субмодели лежит транспортное уравнение, описывающее перенос, где коэффициент диффузии, 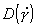 , и нормальная скорость, V(l), представляют функциональные зависимости от поперечной координаты, в безразмерных координатах, l, данное уравнение имеет вид: , и нормальная скорость, V(l), представляют функциональные зависимости от поперечной координаты, в безразмерных координатах, l, данное уравнение имеет вид:
|
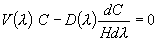 , ,
|
(30) |
где D(l) – коэффициент диффузии, зависящий от скорости деформации и, как следствие, изменяющийся от точки к точке, V(l) – поперечная скорость. Для описания поперечной составляющей скорости, V(l), может быть использована функция, предложенная Берманом в работе [6]. Она имеет вид:
|
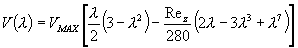 . .
|
(31) |
Для описания зависимости коэффициента диффузии, 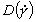 , от скорости деформации, может быть рекомендовано выражение, предложенное Зидни и Колтоном [9, 10, 11], которое имеет вид: , от скорости деформации, может быть рекомендовано выражение, предложенное Зидни и Колтоном [9, 10, 11], которое имеет вид: 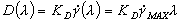 , где KD = 0.03r2. , где KD = 0.03r2.
Подстановка соответствующих выражений для скорости, V(l), и коэффициента диффузии, D(l), в выражение (30) дает выражение концентрационного профиля в процессах микрофильтрации, когда коэффициент диффузии является функцией скорости деформации, 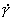 . Функция представлена в l-координатах, где l = 1 – z/H (см. рис. 1): . Функция представлена в l-координатах, где l = 1 – z/H (см. рис. 1):
|
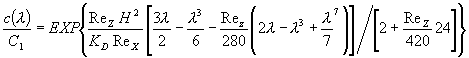 , ,
|
(32) |
где KD = 0.03r2.
Представленная субмодель (32) позволяет анализировать влияние нормальной и тангенциальной гидродинамической составляющих, ReZ и ReX, геометрической полувысоты канала, Н, и радиуса суспендированных частиц, r, на конфигурацию концентрационного поля. Серия расчетных профилей степени КП для плоскорамного мембранного модуля показана на рис. 5.
Субмодель (С3) , описывающая формирование и перемещение слоя геля вдоль фильтрующей поверхности. При моделировании перемещения слоя учитывается его неньютоновское поведение. Данная субмодель построена на основе следующего балансового уравнения:
|
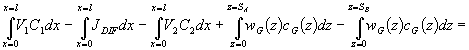 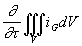 , ,
|
(33) |
где wG(z) – профиль скорости перемещения слоя геля, CG – концентрация геля в слое, принята постоянной и равной концентрации гелеобразования. Транспортные составляющие в выражении (33) проиллюстрированы на рис. 6. В результате преобразований данного выражения получен ряд соотношений в аналитическом виде для количественной оценки скорости формирования слоя и нестационарности процесса. Подробное описание данной субмодели представлено в работе [19].
Группа субмоделей (С4–С5) для описания транспорта через мембрану. Данная группа субмоделей основана на следующих физических предпосылках:
А. Мембрана представляет собой пористое тело, численно характеризуемое такими параметрами, как пористость, удельная внутренняя поверхность, извилистость капилляра, число пор на единице поверхности, а также кривой распределения по размерам f(R). Для аппроксимации плотности вероятности неоднородного распределения пор была использована функция Максвелла f(R) = AMR2 exp(BMR2), где f(R) – плотность вероятности, пропорциональная числу пор, имеющих радиус в интервале между R и R + dR; АM и ВM – параметры функции Максвелла, полученные на основе анализа гистограммы.
В. Жидкость представляет собой неньютоновское тело, при моделировании ее поведения учитываются зависимость вязкости, mN, от скорости деформации (dV/dr), которая аппроксимирована следующей степенной функцией: m(r) = K1(dV/dr)m–1. Для описания течения в индивидуальной поре радиуса R использовано следующее выражение для профиля скорости: 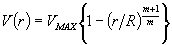 . .
С. Трансмембранный перенос диспергированной фазы. В модели учитывается полидисперсность разделяемой суспензии. Для описания распределения частиц по размерам использована следующая функция [20]:
|
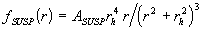 , ,
|
(34) |
где fSUSP(r) – плотность вероятности распределения диспергированной фазы в диапазоне от r до r + dr.
Данная субмодель базируется на “ситовом” механизме разделения, предполагающем размер проникающей частицы меньше размера капилляра. При проникновении через мембрану отсутствует физико-химическое взаимодействие между диспергированной фазой и материалом мембраны. Адсорбция и механическое задержание диспергированной фазы в объеме мембраны пренебрежимо мало. Представленная в работе субмодель позволяет прогнозировать фракционный состав фильтрата и концентрата на основании кривых распределения исходной суспензии и мембраны. Расчетные кривые распределения суспендированной фазы в фильтрате и концентрате приведены на рис. 7. Описание данной субмодели представлено в работе [21].
Субмодель (С6) для описания расчета движущей силы баромембранного процесса. Подход основан на уравнении баланса механической энергии. Подробное описание данной субмодели представлено в работе [22]. Предложенный подход, в отличие от подходов, основанных на балансе импульса, может быть применен в широком диапазоне значений трансмембранных потоков при моделировании процессов в тонкоканальных аппаратах. В основе субмодели лежит уравнение баланса механической энергии в проницаемом канале, где учитывается трансмембранный перенос механической энергии:
|
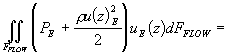
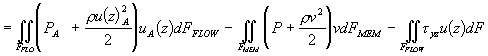 , ,
|
(35) |
где dFMEM = dxdy и dFFLOW = dydz – контрольные сечения для продольного и поперечного потоков. В транспортные интегралы заложена математическая формулировка профиля скорости, учитывающего неньютоновское поведение фазы (см. выражение 6). В результате интегрирования и последующих преобразований получены следующие выражения для оценки соответствующих потоков механической энергии. Поток механической энергии через выходное контрольное сечение (см. левую часть выражения 35) представлен следующим образом:
|
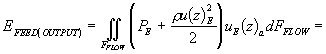
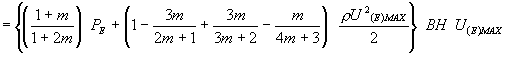 . .
|
(36) |
Выражение аналогичной структуры получено в результате преобразований первого слагаемого правой части, характеризующего приток механической энергии. Подробное описание преобразований представлено в работе [22]. В результате преобразований второго слагаемого в правой части выражения (35) получено выражение для трансмембранного переноса механической энергии:
|
 , ,
|
(37) |
где FMEM = BDL.
Последнее слагаемое в правой части выражения (35) отражает потери механической энергии, в результате преобразований оно записано следующим образом:
|
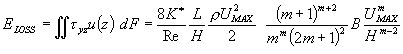 . .
|
(38) |
Субмодель, описанная уравнениями (36–38) и решенная относительно давления в выходном контрольном сечении (Ре), позволяет количественно прогнозировать изменение давления и движущей силы по длине. Серия расчетных значений тангенциального изменения давления при различных реологических показателях степени ( m) представлена на рис. 8.
[ На следующий раздел] [На Содержание] [Условные обозначения] [Подстрочные индексы] [Безразмерные комплексы]
Copyright ©
|
|
 |
 |
Для того, чтобы мы могли качественно предоставить Вам информацию, мы используем cookies, которые сохраняются на Вашем компьютере (сведения о местоположении; ip-адрес; тип, язык, версия ОС и браузера; тип устройства и разрешение его экрана; источник, откуда пришел на сайт пользователь; какие страницы открывает и на какие кнопки нажимает пользователь; эта же информация используется для обработки статистических данных использования сайта посредством интернет-сервисов Google Analytics и Яндекс.Метрика). Нажимая кнопку «СОГЛАСЕН», Вы подтверждаете то, что Вы проинформированы об использовании cookies на нашем сайте. Отключить cookies Вы можете в настройках своего браузера.
Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование
материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
|

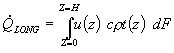 .
.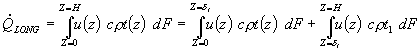 .
.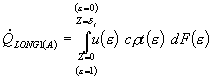 .
. .
.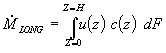 .
.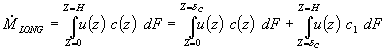 .
.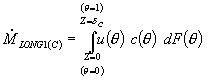 .
.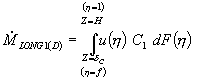 .
.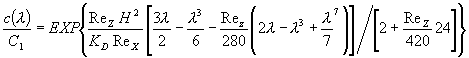 ,
,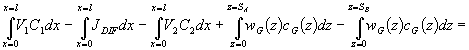
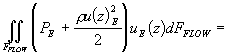
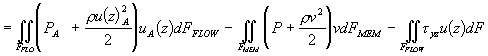 ,
,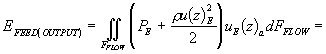
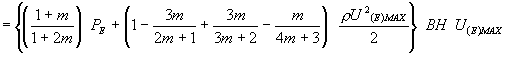 .
. ,
,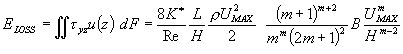 .
.